Nemeth Braille Alphanumerics and Unicode Math Alphanumerics
Both Unicode and Nemeth braille include sets of math alphanumerics. Section 2.2 of Unicode Technical Report #25 discusses the math alphanumerics and why they’re important for math. Microsoft Office math zones use math alphabetics for most variables and support the math digit sets as well. Accordingly, we need mappings between Unicode and Nemeth braille math alphanumerics. This post describes the mappings and discusses how to resolve some incompatibilities between the two standards.
Mappings
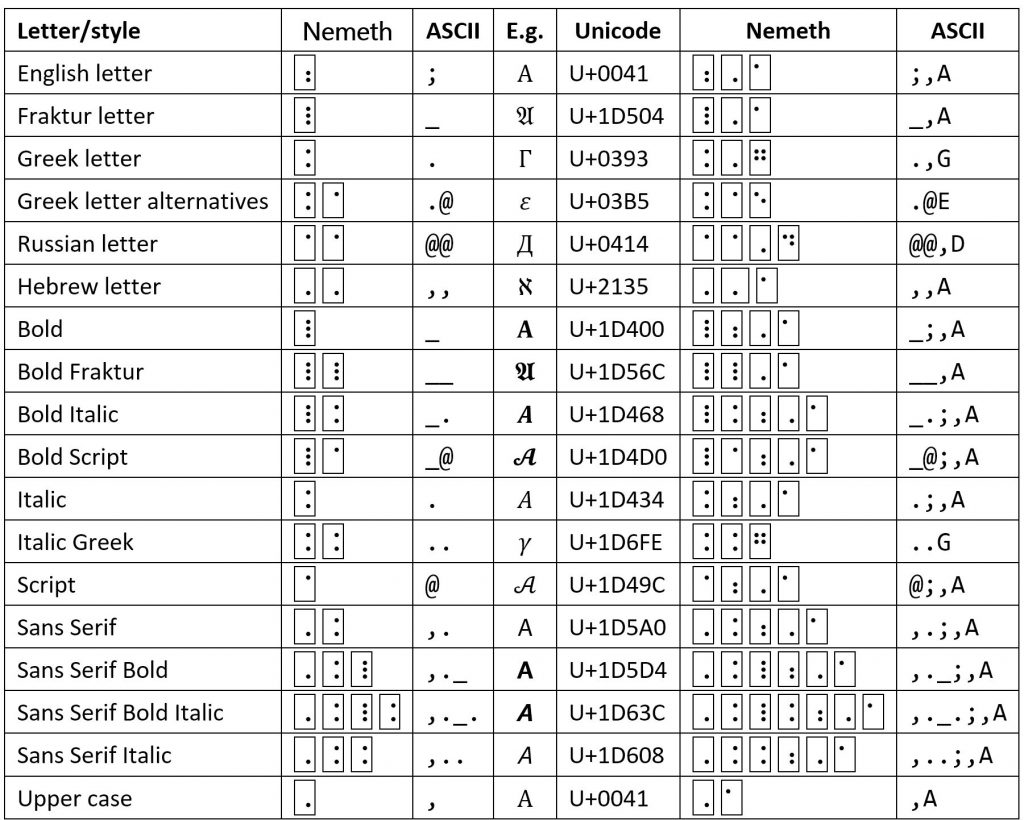
For the most part, the mappings are straightforward as illustrated in the table below. But due to its generative use of type-form and alphabetic indicators, Nemeth braille encodes some math alphabets not in Unicode, e.g., Greek Script and Russian Script. Meanwhile, Unicode has math double-struck and monospace English alphanumerics, which don’t exist in Nemeth braille. Unicode also has six alphabets that aren’t mentioned in the Nemeth specification but that can be defined unambiguously with Nemeth indicators, namely bold Fraktur (Nemeth calls Fraktur “German”), bold Script, and Sans Serif bold and/or italic. The table below includes unambiguous prefixes for these alphabets chosen such that the Nemeth bold indicator precedes the italic or script indicators, and the Sans Serif indicator precedes the bold indicator. These choices correspond to the orders in which the Unicode math alphabets are named. Changes in this ordering result in alternative prefixes that are also unambiguous, but it seems simpler for implementations and users to standardize on the Unicode name ordering.
Greek Alternative Letters
The Nemeth specification has Script Greek (in §22) as well as “alternative” Greek letters (in §23). Some of the latter may be referred to as “script”. Specifically, the Unicode math Greek italic letters 𝜃𝜙𝜖𝜌𝜋𝜅 have the alternative counterparts 𝜗𝜑𝜀𝜚𝜛𝜘, respectively. The symbol 𝜗 can be called “script theta”. Since Unicode doesn’t have a math script Greek alphabet, it makes sense to map Nemeth math script Greek letters to the alternative Greek letters, if they exist, on input and to use the Nemeth alternative notation on output. In addition, in Unicode the upper-case Θ has the alternative ϴ. In TeX and Office math, the alternative letters are identified by control words with a “var” prefix, as in \varepsilon for 𝜀 as contrasted with \epsilon for ϵ. Interestingly, modern Greek uses 𝜑 and 𝜀 instead of 𝜙 and 𝜖, but math considers the script versions to be the alternatives.
Russian Letters
Nemeth braille has several Russian alphabets (see §22 of the Nemeth spec). These alphabets map to characters in the Cyrillic range U+0410..U+044F. Unicode has no math Russian alphabets, but italic and bold Russian alphabets can be emulated using the appropriate Cyrillic characters along with the desired italic and bold formatting. The Unicode Technical Committee, which is responsible for the Unicode Standard, has not received any proposals for adding Russian math alphabets. At least in my experience, technical papers in Russian use English and Greek letters in math zones. In Russian technical documents, this has the nice advantage of easily distinguishing mathematical variables from normal text.
Hebrew Letters
Unicode has four predefined Hebrew characters in the Letterlike Symbols range U+2135..U+2138: ℵ, ℶ, ℷ, ℸ, respectively. In math contexts, it makes sense to map those Hebrew letters in Nemeth braille to the Letterlike Symbols and to map the other Nemeth Hebrew letters to characters in the Unicode Hebrew range U+05D0..U+05EA. The Unicode Technical Committee has not received any proposals for adding more Hebrew math letters so they probably won’t appear in math zones, except, perhaps, as embedded normal text.
Math Digits
The majority of Unicode math digits can be represented by the appropriate type-form indicator sequences in the table above followed by the numeric indicator ⠼ (if necessary) and the corresponding ASCII digits. For example, a math bold 2 (𝟐—U+1D7D0) can be represented by ⠸ ⠼ ⠆ or “_#2”. This works for the bold and/or sans-serif digits, but not for the double-struck and monospace digits, which have no Nemeth counterparts. Meanwhile Nemeth notation supports italic and bold italic digits, which aren’t in Unicode.
Digits in some math contexts don’t need a numeric indicator, e.g., most digits in fractions, subscripts or superscripts. To optimize common numeric subscript expressions like a1, the numeric indicator and the subscript indicator are omitted. In Nemeth ASCII braille, a1 is “A1” and in Nemeth braille it’s ⠁ ⠂ . The ASCII braille representation is tantalizing since variables like A1, B2, etc., are used to index spreadsheets and it would be more natural if spreadsheet indices were a1, b2, etc., at least for people with a mathematical background.
Conclusions
In general, Unicode’s math characters are simpler to work with since they can be assigned separate character codes instead of being composed as combinations of 64 braille codes. Unicode has about 2310 math characters (see Math property in DerivedCoreProperties.txt) and to distinguish all of those without indicators would require 12-dot braille! Such a system would be really hard to learn. LaTeX describes characters using control words consisting of a backslash followed by combinations of the 64 ASCII letters. That approach has mnemonic value, but it’s not as concise as the Nemeth braille character code sequences. When you get a feel for the Nemeth approach, a character’s Nemeth sequence gives a good idea of what a character is even if you haven’t encountered it before. UnicodeMath and Nemeth braille are intended to be read by human beings, whereas LaTeX and MathML are intended to be read by computer programs, notwithstanding that some TeXies can read LaTeX pretty fluently! Considering that Unicode math alphabets like double-struck and monospace aren’t yet defined in Nemeth braille, it would be worthwhile to choose appropriate type-form indicators for them. Nemeth math alphabets not in Unicode probably don’t have to be considered unless they show up in published documents.