音声再生速度変換 : もっとゆっくりしゃべって!
こんにちははらだんです。どういうわけか最近お問い合わせが増えている音声再生速度の変換(タイムストレッチ)についてお話します。
皆さんの中には以下のような思いをしたことある人いませんか?はらだんはしょっちゅうあります。
・会議の録音をタイプするためにゆっくり聞きたい。
・英語の勉強のためにゆっくり/早く再生したい。
・音楽をミミコピ(採譜)したいのでスローテンポで聞きたい。
こういう時に例えば WAV ファイルのヘッダ情報のサンプリングレートのパラメータだけをいじると確かに再生速度は変えられますが、音程(音の高低)が変わってしまうのです。逆に聞き取りづらくなってしまいます。音楽に至っては致命的です。
今回は「音程を変えずに再生速度を変えたい!」という、いわゆるタイムストレッチを実現するための原理の概要を説明したいと思います。
実は Windows Media Player SDK (Windows SDK に含まれています)にある IWMPSettings::put_rate を使用すると再生速度変換はそのものずばり実現できてしまいます。これは、Windows Media Player の[表示] - [拡張設定] - [再生速度の設定] で設定できる再生速度と同じ機能なので、とりあえず試しに聞いてみてください。
聞いて頂ければわかりますがお世辞にもこの機能の音質はいいとは言えない・・・のです。なにかこう音がダブる感じに聞こえませんか。
さらにコンテンツのコンテナにも依存します。WMA, MP3 ファイルは対応していますが、WAVファイルは対応していません。
WMP をホストする形でのアプリケーションとなることからも、独自の実装を行うプレーヤを開発する場合や、DirectShow / MF のフィルタを作成しようという場合には使えません。たいへん残念なことに API として汎用的にこれを実現できるような便利な関数は提供されていません。(つまり方法をお問い合わせいただいても残念ですがここまでの回答となります。そういう理由で Blog にてお話しすることになりました。)
ずばり自作する必要があるでしょう。どうせ作るなら Windows Media Player のものよりいい音で再生したいところです。
そうは言ってもまずは原理から知らないと実現できませんので、こんな感じ☆とご紹介します。
興味が沸いたらチャレンジしてみてください。
以下の章立てでご紹介します。
1. タイムストレッチの原理
2. 一周期の長さは?
3. 自己相関関数
4. 自己相関関数で速度変換
5. 畳込み計算(のりしろ)
6. 参考文献
1. タイムストレッチの原理
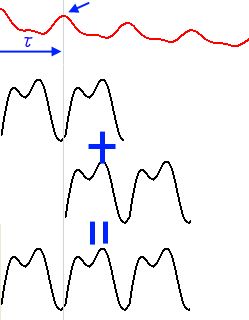
以下のような波形(sin波ですが)を音程を変えずに再生時間を変更することを考えます。図の縦方向は振幅を、横方向は時間を表わしています。赤い矢印はこの音の一周期分の時間を指しています。
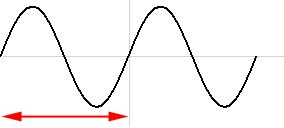
以下の 2 つはどうでしょうか?これはサンプルデータ自体は手を加えずにサンプリングレートのみを調整したものです。例えば 44kHz のサンプリングレートである所を 33kHz あるいは 66kHz と思って再生するとこのようになります。
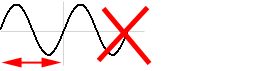

×と書いたのでこれが間違えであると激しくネタばれしていますが、1 つ目は再生時間が半分の早送り再生です。しかしこれは音程が高くなります。 2 つ目は再生時間が 2 倍になるスロー再生ですが、こちらは音程が低くなります。
赤い矢印が一周期分の時間と先ほど書きましたが、この逆数 1/[一周期の時間(s)] が周波数(Hz)です。"音程を変えない"ということはこの長さが変わらないということを意味します。
以下のように一周期の波形をほしい時間分追加すると音程を変えずに再生時間を長くすることが出来ます。(この場合 1.5 倍の再生時間のスロー再生です)短くする場合は必要なだけ一周期分削除します。
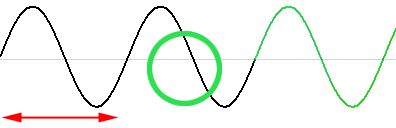
原理はこれだけ!一言で言うならコピペですよ旦那。カ・ン・タ・ン☆
2. 一周期の長さは?
さてここで問題です。
実際の人の声や音楽はこんなに簡単な波形ではありません。音程は逐次変化するし、広い周波数帯域にわたって音は出ています。どこを一周期とみなして切り貼りしたらよいのでしょう。
どこからどこまでが一周期とはなかなか言えません。1 つの答えはある区間を一周期とみなし、強引に決めた区間をコピペすることです。
たとえば以下のような具合になります。これでもまだシンプルな波形です。実際には複雑かつもっと先までずっと続いているわけですが、コピーして一定の区間 (τ サンプル)だけずらして合成する。これを繰り返します。
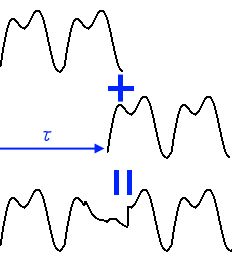
結果は図の一番下の波形です。残念な感じであることがわかると思います。(ちょっと図が変な気がしますが、こんな感じだと思ってください)
3. 自己相関関数
周期性を利用しないとだめだろうということで、次は周期性を見つけることを考えます。先程の例の場合、小さい波形はともかく大きな波形は
見た感じなんか周期的と見えませんか?大きな波形は 2 周期分ありますね。これが音程として聞こえる波形と考えてこれを検出してみます。
ここではそのために自己相関関数というものを使います。突然出てきましたが、一般にこの方法がよく使われるようです。
どういうものかといいますと、関数 f(t) とその少し時間をずらした関数 f(t+τ) がどれくらい相関があるかを評価できる関数です。
要するに自分がほんのちょっと過去(あるいは未来)の自分にどれくらい似ているのか? という関数です。
人で言うなら髪の毛を切ろうが、1 日で 1kg 太ろうが、次の日服が違おうが、その程度では同じとみなせるのでそういう意味で自己相関性は高いw。 でも何年もあってないとびっくりするぐらい別人てこともたまにはあります。時間がたちすぎると相関性は低くなるのです。
つまり周期がどれくらいかを評価します。sin 波の場合一周期分だけ、時間(τ)をずらすとぴったり関数 f(t) と f(t+τ) が重なります。sin(t) の自己相関関数を計算するとτが丁度一周期分の時間になります。相関関数を式であらわすと以下のようになります。
Arr(τ) = ∑ ( f(t) * f(t+τ) )
ここで計算した Arr(τ) は τ=0 の時が最大値となります。τ=0 は自分自身なので似ているどころか同じだからです。
4 . 自己相関関数で速度変換
下の図の赤いグラフが自己相関関数の例です。青の矢印の位置のピークが見つけたいτです。よーく見ると青い文字でτと書いてあるあたりにも局所的なピークが見れますが、これは"ちょっと似ている"という位置です。無視します。青い矢印のある関数の 2 つ目のピークの位置τが周期となります。この位置で波形をつなげると図のように奇麗につながります。( 1 つ目のピークは τ=0 )
この例ではピークが見つけやすいのですが、たとえば振動のある波形(Qがあるとか言いますが、後で図を用意したいと思います)などの自己相関関数は非常にたくさんのピークを持ち、1 つを決めるのが困難となります。それがこの方法の弱点ですが、FFTで周波数を探したとしても同じことです。
注意点は最大値ではなく最大のピークを見つけることです。ピークは微分が正から負に変わるところですね。離散化されたデータの場合ざくっと言うと隣のデータとの差です。それだけだと実際のデータでは結構ハズレを引きます。
それから、対象とする音がある程度分かっている時、特に単一の音声の場合には周波数の範囲を限定することができると思います。例えば 500Hz~7kHz くらい等。τはこれに関連しますので、1/τ がこの範囲になる所だけを計算すればよく、ずっと計算し続ける必要はありません。実際には離散化されていますので、プログラム上ではτは τ=n*(1/Fs) と表せます。n はずらしたサンプル数。Fs はサンプリング周波数です。
τが小さいと周期が短いので、高い周波数を主に持つ音(高い音程の音が鳴っている)となります。
原理としてはこんなところです。自己相関に限らず、周期性を利用してコピペする方法は何も考えずにコピペするよりはましだけど完全ではありません。いろんな音程が混ざっている時にはそのうちの 1 つにしかフォーカスできないからです。声だけならまだよいかもしれません。音楽となると厳しいということが予想できると思います。
5 . 畳込み計算(のりしろ)
通常波形のつなぎ合わせの際には、いきなりつなげないで重ねてつなぎます。言うなれば"のりしろ"です。この重なる部分は前半の波形は段々減衰させ、後半部分の波形は段々増幅していくようにすることで継ぎ目なく合成します。クロスフェードというほうがイメージしやすいでしょうか?
(相関の低い部分で、この"のりしろ"がそこそこの時間を持っているとその区間は音がダブって聞こえることが予測できます。)
以下の例では直線的な減衰を行っています。他にも cos 波、FFT の際によく出てくるハニング、ハミング、ブラックマンなど、方法はいくつかあります。ここで使う関数を窓関数と呼びます。
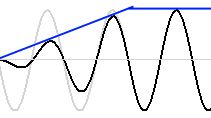
この例はのりしろで貼りつける後半部分の計算例です。
グレーの sin 波が元の波形、青い線が窓関数で、0.0~1.0 に直線的に変化するものです。これをグレーの波形に掛けて黒い波形を作成します。
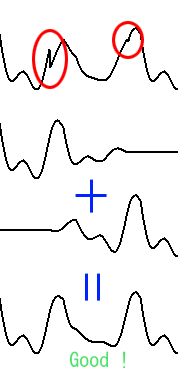
窓関数を使用した場合としなかった場合の比較を行いましょう。以下の図の最初の波形では赤い丸で囲んだ部分に不連続が発生しています。これを聞くと非常に不快な音が混じります。真ん中の 2 つの波形が窓関数を使用した後の波形です。これらを合成すると一番下の波形となります。不連続部分が解消されるのが分かると思います。
6 . 参考文献
最後に超参考になる文献を紹介しておきます。
・C magazine 2000 年 3 月号 特集 2
おそらくすでに雑誌は手に入りませんのですべての号が収録された PDF 版の「まるまる C magazine」を入手する必要があります。
・トランジスタ技術 2009 年 1 月号 : 特集
今ならまだバックナンバーで入手が可能だと思います。
・C言語ではじめる音のプログラミング サウンドエフェクトの信号処理青木直史
ISBN 978-4-274-20650-4
この本にはサンプルコードもありすぐに試せると思います。
DirectShow フィルタや MFT 等の作成に挑戦して使い方の不明な SDK の関数などございましたら私たちサポートまでお問い合わせください!
それにしてもどうして最近急にタイムストレッチの問い合わせが増えているのか謎です。
~どんなにゆっくり聞いても知らない単語は聞き取れないはらだん~