UNISA Chatter – Formal Logic: Propositional Logic Conditional Symbols
See UNISA – Summary of 2010 Posts for a list of related UNISA posts. This post is one of the summary posts I will be building up over the next couple of months, so if you are following this topic or completing the same course as I this year, you may want to bookmark this post and come back occasionally for a peek and to give “candid” feedback.
The following truth tables summarise the main conditional symbols used as part of first-order-language (FOL):
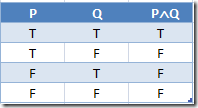
Conditional Symbol Ù
In English we typically use terms such as and, moreover and but. Also known as the conjunction symbol.
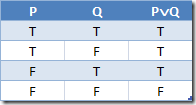
Conditional Symbol Ú
In English we typically use the term or. Also known as disjunction symbol.
Conditional Symbol Ø
When using English we typically use terms such as not, it is not the case, non- and un-. Also known as the negation symbol.
See UNISA Chatter – Formal Logic: Propositional Logic Proofs for examples using the three symbols covered above.
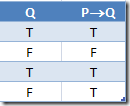
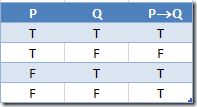
Conditional Symbol ®
Also known as the material conditional symbol, it states that P®Q is true if and only if either P is false or Q is true, or both.
P®Q could be expressed as ØP Ú Q.
We will cover this one in this post and work through an example which gave me nightmares for days … then suddenly it clicked.
Some basics first.
If we have to prove a one (®) directional conditional symbol, the process is as follows:
- If the goal is to show that P®Q, then …
- Sketch a sub proof with P as an assumption and Q as the final step
- Q will become intermediate goal while checking the proof and by proving that we can rely on assumption P
- Example …

If we have a bidirectional situation («), the process changes to:
- If the goal is to show that (P®Q)«(ØP®ØQ), then …
- Sketch the two sub proofs ahead of time, i.e. P®Q and ØP®ØQ
- Cite the sub proof in support
- Fill the sub proofs, which could become long.