UNISA Chatter – Formal Logic: Propositional Logic Summary
See UNISA – Summary of 2010 Posts for a list of related UNISA posts. This post is one of three summary posts I will be building up over the next couple of months, so if you are following this topic or completing the same course as I this year, you may want to bookmark this post and come back occasionally for a peek and to give “candid” feedback.
** UNDER CONSTRUCTION ** Last change: 2010-04-05
Summary
The eye of this excursion is the first-order logic (FOL) language which goes back to Aristotle and is used by a variety of environments such as mathematics, philosophy, linguistics and artificial intelligence.
 |
 |
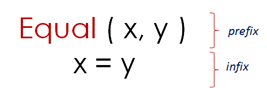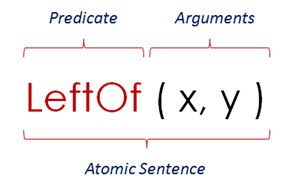
The two examples above are referred to in the terminology summary below:
| Terminology | Description | Example |
| Arity | Defines how many names|constants a predicate needs. Unary = 1, Binary = 2, … | LeftOf(x,y) … Arity = 2 Planet(pluto) … Arity = 1 |
| Atomic Sentence | Is a predicate followed by the right number (arity) of names | Bigger(saturn,pluto) Sentence –> Pluto is a planet Atomic sentence –> Planet(pluto) |
| Constant | Symbols used to refer to a specific object, analogous to names, and written in lowercase. | pluto |
| Conclusion | Is a logical consequence of premises. | |
| Conjunctive Normal Form (CNF) | A sentence is in conjunctive normal form (CNF) is it is a conjunction of one or more disjunctions of one or more literals. | See UNISA Chatter – Formal Logic: Propositional Logic Proofs for a proof | an example. |
| Disjunctive Normal Form (DNF) | A sentence is in disjunctive normal form (DNF) is it is a disjunction of one or more conjunctions of one or more literals. | See UNISA Chatter – Formal Logic: Propositional Logic Proofs for a proof | an example. |
| Identity Introduction | Rule that embodies the reflexity of identity | | n = n = Intro |
| Identity Elimination | Rule that embodies indiscernibility of identicals | | 1. P(n) | 2. n = m | 3. P(m) = Elim 1,2 |
| Indiscernibility of identicals | Also known as substitution. | If b = c, then anything is true of b is also true of c. |
| Infix Notation | With infix notation the predicate appears between two arguments | x = y |
| Informal proofs of non-consequence | Possible situation were premises are true, but conclusion is false. See UNISA Chatter – Formal Logic: Propositional Logic Examples for more examples. | | Nearly all soccer players are funny true | Grumpy plays soccer true |-- | Grumpy is funny false |
| Logical Truth | Necessity | X is logically necessary if and only if it is impossible for X to be false. | See UNISA Chatter – Formal Logic: Propositional Logic Proofs for a proof | an example. |
| Logical Equivalence | X and Y are logically equivalent if and only if it is impossible for either of them to be true and the other false. | See UNISA Chatter – Formal Logic: Propositional Logic Proofs for a proof | an example. |
| Logical Consequence | X is a logical consequence of Y1, Y2, …Yn if and only if it is impossible for Y1, Y2, … Yn to be true and X is false. | See UNISA Chatter – Formal Logic: Propositional Logic Proofs for a proof | an example. |
| Negative Normal Form (NNF) | A sentence is in negative normal form (NNF) if all occurrences of Ø apply directly to atomic sentences. | See UNISA Chatter – Formal Logic: Propositional Logic Proofs for a proof | an example. |
| Object | Anything that we can make claims about | Jupiter, Pluto, Carola |
| Prefix Notation | With prefix notation the predicate precedes the arguments | Equal(x,y) |
| Predicate | Expresses properties of an object or relations between objects | Equal, LeftOf, … |
| Proof | A step-step demonstration that a conclusion follows from some premises, using either a formal or informal style. | Informal proof Since CTOS is an operating system and all operating systems crash, it follows that CTOS will crash. Formal proof | 1. Square ( a ) | 2. a = b |-- | 3. Square ( b ) |
| Quantifiers | Also see “Symbols” below Distribution " through Ù Distribution $ through Ú Null Quantification Bound variable replacement DeMorgan Laws | "x(P(x) Ù Q(x)) <=> "xP(x) Ù "xQ(x) $x(P(x) Ú Q(x)) <=> $xP(x) Ú $xQ(x) "x(P Ú Q(x)) <=> P Ú "xQ(x) $x(P Ù Q(x)) <=> P Ù $xQ(x) "xQ(x) <=> "yQ(y) $xQ(x) <=> $yQ(y) Ø"xQ(x) <=> $yØQ(y) Ø$xQ(x) <=> "yØQ(y) Øx($(x) Ù "Q(x)) <=> Ø$xP(x) Ú Ø"xQ(x) "x(P(x) ® Q(x)) <=> "x(ØP(x) Ú Q(x)) <=> "xØ(P(x) Ù ØQ(x)) Ø"x(P(x) ® Q(x)) <=> $x(P(x) Ù ØQ(x)) Ø$x(P(x) Ù Q(x)) <=> "x(P(x) ® ØQ(x)) |
| Reflexity of identity | Sentences of the form a = a are always true | |
| Reiteration | Repeat an earlier step | | 1. n = n | … | 2. n = n = Reit 1 |
| Soundness | Implies that a deductive argument is both valid and that all premises are true. See UNISA Chatter – Formal Logic: Propositional Logic Examples for more examples. | Valid argument, which is not sound | All proprietary operating systems are expensive | CTOS is a proprietary operating system |-- | CTOS must be an expensive operating system … why? Because first premise is false. |
| Rules | Typical rules used as part of proofs, DNF or CNF formatting includes:
|
Ø[(ØA Ù B) Ú Ø(C Ú ØD)] = Ø(ØA Ù B) Ù Ø[ Ø(C Ú ØD)] De Morgan = Ø(ØA Ù B) Ù (C Ú ØD) Elim ØØ = (ØØA Ú ØB) Ù (C Ú ØD) De Morgan = (A Ú ØB) Ù (C Ú ØD) Elim ØØ = [(A Ú ØB) Ù C] Ú [(A Ú ØB) Ù ØD] Distribution = [C Ù (A Ú ØB)] Ú [ØD Ù (A Ú ØB)] Commutativity = [(C Ù A) Ú ( C Ù ØB)] Ú [(ØD Ù A) Ú ( ØD Ù ØB)] Distribution = (C Ù A) Ú ( C Ù ØB) Ú (ØD Ù A) Ú ( ØD Ù ØB) Indempotence --> DNF format |
| Symbols | Ø Negation … not ¹ Nonidentity … is not Ù Conjunction … and, moreover, but Ú Disjuntion … or ® Conditional … if, if then « Conditional … if and only if, iff " Quantifier … all, everything $ Quantifier … something, at least one | Ø Planet(monkey) Pluto ¹ Saturn Planet(pluto) Ù Planet(saturn) Planet(moon) Ú Planet(saturn) All P’s are in Q … "x(P(x) ® Q(x)) Some P’s are in Q … $x(P(x) Ù Q(x)) No P’s are in Q’s … $x(P(x) ® ØQ(x)) Some P’s are not in Q’s … $x(P(x) Ù ØQ(x)) |
| Symmetry of identity | If b = c then c = b | |
| Tautology | X is a tautology if and only if every row of its truth table is true. | See UNISA Chatter – Formal Logic: Propositional Logic Proofs for a proof | an example. |
| Tautology Consequence | X is a tautological consequence of Y1, Y2, …Yn if and only if there is no row in the joint truth table in which Y1, Y2 … Yn are all true and X is false. | See UNISA Chatter – Formal Logic: Propositional Logic Proofs for a proof | an example. |
| Tautology Equivalence | X and Y are tautologically equivalent if and only if there is no row of their joint table in which one value is true and the other is false. | See UNISA Chatter – Formal Logic: Propositional Logic Proofs for a proof | an example. |
| Transitivity of identity | If a = b and b = c, then a = c | |
| Truth Value | The truth value value of a statement is true if the statement is true in the circumstances, else the truth value is false. | |
| Validity | Validity implies that there is no possibility in which premises are true and the conclusion false. See UNISA Chatter – Formal Logic: Propositional Logic Examples for more examples. | Valid and sound argument | LeftOf ( x, z ) ;Premise | LeftOf ( x, y ) ;Premise |-- | LeftOf ( y, z ) ;Conclusion |
Some of these expressions and proofs are a real tongue twister … but formal logic is fun … so far :)