UNISA Chatter – Formal Logic: Propositional Logic Proofs

  • Article

See UNISA – Summary of 2010 Posts for a list of related UNISA posts. This post is one of three summary posts I will be building up over the next couple of months, so if you are following this topic or completing the same course as I this year, you may want to bookmark this post and come back occasionally for a peek and to give “candid” feedback.

** UNDER CONSTRUCTION ** Last change: 2010-01-27

This post contains a collection of examples, sorted alphabetically by title, referred to from UNISA Chatter – Formal Logic: Propositional Logic Summary.

ØÙÚ … these are copy|paste placeholders while we are working on this post.

Conjunctive Normal Form (CNF)

A sentence is in conjunctive normal form (CNF) is it is a conjunction of one or more disjunctions of one or more literals.

(A Ù B) Ú (C Ù D)

…

  1. [(A Ù B) Ú C] Ù [(A Ù B) Ú  D]
  2. (A Ú C) Ù (B Ú C)  Ù [(A Ù B) Ú  D]
  3. (A Ú C) Ù (B Ú C)  Ù (A Ú D) Ù (B Ú D) … CNF

Disjunctive Normal Form (DNF)

A sentence is in disjunctive normal form (DNF) is it is a disjunction of one or more conjunctions of one or more literals.

(A Ú B) Ù (C Ú D)

…

  1. [(A Ú B) Ù C] Ú [(A Ú B) Ù  D]
  2. (A Ù C) Ú (B Ù C)  Ú [(A Ú B) Ù  D]
  3. (A Ù C) Ú (B Ù C)  Ú (A Ù D) Ú (B Ù D) … DNF

Informal Proof of an argument

image

  • We get the desired goal or conclusion if Carol is happy
  • Premises
    1. Either Max or Claire are home
    2. Max is not home or Carl is happy
    3. Claire is not home or Carl is happy
  • If we assume in premise 1, that Max is home, then Claire is not.
  • In premise 2 we are saying that either Max is not home or Carl is happy.
    • --> So it must be that Carl is happy

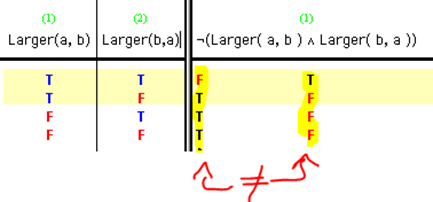
Logical Truth

X is logically true | necessary if and only if it is impossible for X to be false.
a=a is a great example.

image

The sentence  Ø(Larger(a,b) Ù Larger (b,a)) cannot possibly be false, i.e. it is logically necessary, but not a tautology.

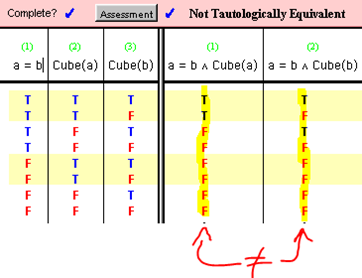
Logical Equivalence

X and Y are logically equivalent if and only if it is impossible for either of them to be true and the other false.

Consider the sentences:

  • a = b Ù Cube(a)
  • a = b Ù Cube(b)

Proof 1 for logical equivalence:

  1. Suppose a = b Ù Cube(a) is true.
  2. Then, a = b is true and Cube(a) is true.
  3. Using indiscernibility of identicals or identity elimination (If b = c, then anything is true of b is also true of c) we know that Cube(b) is also true.
  4. Therefore a = b Ù Cube(a) logically implies the truth of a = b Ù Cube(b)

Proof 2 for logical equivalence:

  1. Suppose a = b Ù Cube(b) is true.
  2. Then, a = b is true and Cube(b) is true.
  3. Using symmetry of identity (If b = c then c = b) we know that  b = a
  4. From this and Cube(b) we can conclude that Cube(a) is also true.

Test for tautology:

image

As shown, a logical equivalence is not necessarily tautological equivalent, although the reverse always applies.

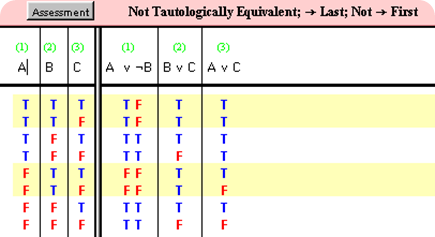
Logical Consequence

X is a logical consequence of Y1, Y2, …Yn if and only if it is impossible for Y1, Y2, … Yn to be true and X is false.

Example:

Is A Ú C is a consequence of A Ù ØB and B Ú C?

image

In rows 1, 2, 3 and 7  the last sentence is true, together with the first and second. Therefore  the last is a tautological consequence and therefore logical consequence of (1) and (2).

Negative Normal Form

Ø((A Ú B) Ù ØC) is not a NNF sentence.

…

  • Ø(A Ú B) Ú ØØC
  • Ø(A Ú B) Ú C
  • (ØA Ù ØB) Ú C … is NNF

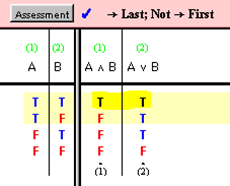
Tautological Consequence

X and Y are tautologically equivalent if and only if there is no row of their joint table in which one value is true and the other is false.

Example:

Is A Ù B  a consequence of A Ú B?

image

We note that the second sentence is a consequence of the first, but the first is not a consequence of the second.

Tautology

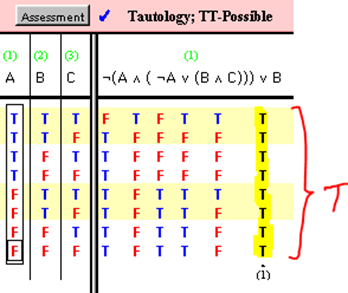image (1) is a tautology if and only if every row of its truth table is true.

Tautology Equivalence

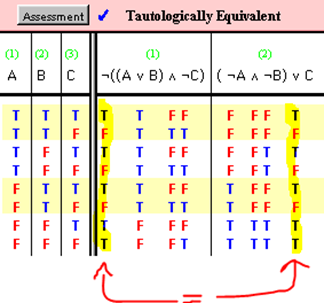image  (1) and (2) are tautologically equivalent if and only if there is no row of their joint table in which one value is true and the other is false.