UNISA Chatter – Formal Logic: Propositional Logic Examples
See UNISA – Summary of 2010 Posts for a list of related UNISA posts. This post is one of three summary posts I will be building up over the next couple of months, so if you are following this topic or completing the same course as I this year, you may want to bookmark this post and come back occasionally for a peek and to give “candid” feedback.
** UNDER CONSTRUCTION ** Last change: 2010-01-27
This post contains a collection of examples referred to from UNISA Chatter – Formal Logic: Propositional Logic Summary.
Associativity
- (A Ù B) Ù C = A Ù (B Ù C)
- (A Ú B) Ú C = A Ú (B Ú C)
De Morgan
- Ø( A Ú B) = ØA Ù ØB
Idempotence
- A ÙB ÙA = A Ù B
- A ÚB ÚA = A Ú B
Distribution
- A Ù ( B Ú C) = (A Ù B) Ú ( A ÙC)
- A Ú ( B Ù C) = (A Ú B) Ù ( A ÚC)
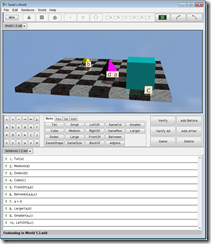
Tarski’s World
The following screen snippet shows Tarski’s World, which is a tool called Tarski’s World used to represent simple, three-dimensional worlds inhabited by geometric artefacts, as well as ability to define and test first-order sentences.
At this stage I am not sure how many more summary posts will be created, but there will definitely be more and a few updates to this post as we plough through the material :)
Some examples …
Translating a formal proof to an informal proof
1. Formal Proof | RightOf ( w, x )
| LeftOf ( y, z )
| w = y
|--
| LeftOf ( x, z )2. Informal proof
According to the formal proof we are told that w is to the right of x, which means that x is to the left of w, since right of and left of are inverses of each other. Since w is equal to y, x is left of y, by indiscernibility of identicals. We are also told that y is left of z, consequently x is left of , by the transitivity of left of.
Interpreting sentences
1. T1 and T2 are not related
2. T3 is T1’s father
3. T3 is not T2’s fatherDoes (3) follow from (1) and (2)?
Yes.
Since T3 is T1’s father, they are related. Since T1 and T2 are not related, T3 cannot be T2’s father.Does (2) follow from (1) and (3)?
No.
We can have a situation where T3 is T1’s father; and T1 and T2 are cousins. In this case (2) and (3) are true, but (1) is false.Does (1) follow from (2) and (3)?
No.
We can have a situation where T3 is T1’s father, but not T3’s and T1 and T3 are cousins. It therefore follows that (2) and (3) are true., but (1) is false.
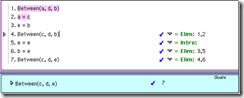
Fitch Formal Proof
1 - 3 Premises
4 – 7 Follow logically from premisesProof:
| 1. Between ( a, b, c )
| 2. a = c
| 3. e = b
| ---
| 4. Between ( c, d, b ) = Elim: 1,2
| 5. e = e = Intro
| 6. b = e = Elim: 5,3
| 7. Between ( c, d, e ) = Elim: 4,6
Determine Soundness and Validity of an argument
All computer developers are clever. Anyone who knows how to program a computer is a developer. Gnumpf is clever. Therefore Gnumpf knows how to program a computer.
- Validity
- false
- imagine two developers, both of which are clever, but only one of which can program. In this case the premises are true, but conclusion false … hence invalid.
- Soundness
- false
Sentence file versus World
![image_thumb21[1] image_thumb21[1]](https://msdntnarchive.blob.core.windows.net/media/TNBlogsFS/BlogFileStorage/blogs_msdn/willy-peter_schaub/WindowsLiveWriter/UNISAChatterFormalLogicPropositionalLogi_10A26/image_thumb21%5B1%5D_1f886460-9fab-4267-8709-3e5faabc9354.png) |
--------->>>> |  |
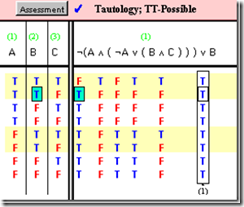
Tautology and truth table using Boole Program