Measuring incremental efficacy and the value of statistics
Inspired by my previous post on measuring false positives, and spam effectiveness, I thought I’d take a look at how to measure incremental value.
In our own organization, we are constantly tweaking things here and there. If we push up the aggressiveness of this filter, we get a few more blocks. If we decrease it, we lose a few blocks. But curiously, if we increase the aggressiveness of another filter, we lose a few blocks. Or if we decrease the aggressiveness, we lose other blocks. What’s going on? Why does changing a filter’s settings result in random behavior? And on the other hand, if we push up the aggressiveness of one filter and it gets more blocks the next day, how do you know that it was that filter that was responsible for increased blocks? Maybe spammers just had a bad day. How can you know for sure what you are doing is actually making a difference and what you are seeing is not random noise? After all, we see billions of messages each day. An extra 100,000 blocks in a blocklist from day-to-day is 0.005% of the total mail stream. That’s a rounding error. Given such large numbers, daily variance is normal. How can you be sure that what you are doing is not contained within the margin of noise?
In fact, what is happening is explained by statistical distribution. The fact is that in large data sets like what we have, we can always expect there to be variance on a day-to-day basis. For example, if we use Spamhaus’s XBL and it blocks 35% of our mail one day and 38% the next day, does it mean that Spamhaus’s list has gotten better? If it drops to 33% the next day, does it mean that it has gotten worse?
The answer is “it depends.” It depends on how many blocks the XBL makes on a daily basis over a particular period of time. Suppose that I had 200 days worth of data, and each data point was how much mail the XBL blocked. Furthermore, let’s assume that nothing changed in the filter to significantly altar how much mail it blocked (i.e., the total amount of mail hitting it remains the same and the order in which it is applied is the same). Suppose the past seven days looks like the following:
Day 1 – 35%
Day 2 – 38%
Day 3 – 40%
Day 4 – 36%
Day 5 – 35%
Day 6 – 36%
Day 7 – 37%
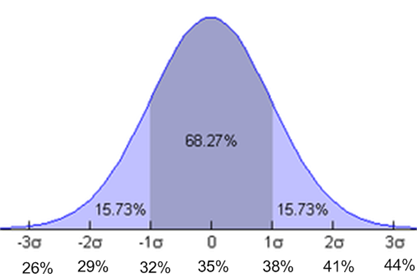
I do this for all 200 days and then I count up how many days occur at each percentage. For example, 35% occurs 75 times, 36% occurs 25 times, 37% occurs 12 times, etc. The reason I do this, of course, is to form a bell-curve distribution. This isn’t a post about statistics (read an article on it elsewhere on the web), but almost all observations follow a normal distribution. In this case, 35% is the mean. In our example, let us suppose that 3% is the standard deviation, denoted σ (mathematicians love Greek symbols to denote stuff). According to statistical theory, approximately 68% of all observations fall between 1 standard deviation above and below the mean. About 95% of the observations fall between 2 standard deviations above and below the mean, and 99% of observations fall between 3 standard deviations above and below the mean.
In the picture below, I have mapped zero to be the mean which is 35% and tacked on the standard deviations on both sides.
What this predicts is that on any given day, there is an approximately 2 in 3 chance that the effectiveness of the XBL is going to be between 32% and 38%. This is simply due to random variance. The list is more effective on some days than other days. However, suppose that one day you saw an observation wherein the list was 42.2%. How random is this?
Well, to do that you would look at the area under the curve. 42.2 – 35 = 7.2% above the mean which represents 2.4 standard deviations above the mean. According to the area under the curve, 98% of all observations fall between 27.9% and 42.1%. This means that the odds of this particular measurement of XBL’s effectiveness has a 2% chance of occurring by chance. So, while it is possible that this is just a random fluctuation of this list’s effectiveness, it is much more likely that something has changed. Either the list has gotten better or something else in the pipeline has gotten worse. Either way, you can be fairly certain that what you are seeing is legitimate and represents really change.
How do you know what level to pick as the cut off for something actually changing? That is to say, if the area under the curve is 94%, can we be confident that it is not random variance? The answer that I give is that the standard for defining something as not random chance is 1 in 20. If the observation you are seeing is outside of 2 standard deviations, then you can be confident that it did not occur by chance (it’s actually closer to 1.95 but two is a good rule-of-thumb).
So, to determine if a new filter you are deploying is actually doing anything, at least in our environment, here’s how I do it:
Collect at least 100 observations (the more the better) in a stable environment measuring how effective something is, up to but excluding the date where you made the change.
Calculate the average value of the observation set.
Calculate the standard deviation of the observation set.
If the measurement from the date you made the change is less than the average + two standard deviations of historical data, then you cannot be sure that what you are seeing is not random noise, at least not from a statistical point-of-view (and assuming you have large data sets where things get lost in the noise of large numbers).
We filter a lot of mail and it is hard to measure efficacy, but properly done and measuring stuff relative to itself, it is possible to pull out valid numbers from data and get an accurate measure of how well changes you made are doing.