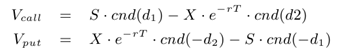F# Black-Scholes running on GPUs and SSE3 Multicore Processors using Accelerator
The Accelerator library from Microsoft helps us write code which can execute on GPUs and multicore processors using SSE3 vector instructions. There is also an experimental FPGA target. To illustrate data-parallel programming in F# using Accelerator I show below an implementation of the Black-Scholes computation which is based on the sample from the CUDA SDK by Victor Podlozhnyuk at NVIDIA and we also draw inspiration from Geoff Mainland's Haskell reformulation of this sample. The objective of this blog is to give you a feel for what data-parallel programming looks like with the Accelerator system.
We shall use the functional language F# to implement both the sequential software version of Black-Scholes and also the data-parallel version using the Accelerator library. Although the code in this blog is written in F# it could also have been written in C++, C#, VisualBASIC, IronPython or Haskell or any language that supports C interop (Accelerator is simply a DLL with corresponding managed wrappers).
In F# an Accelerator program typically starts by importing the Accelerator library Accelerator.ParallelArrays and then by defining some abbreviations for the types of Accelerator data-parallel arrays (e.g. FPA for single precision floating point arrays) and a class ParallelArrays that contains several useful static methods over data-parallel arrays:
open Microsoft.ParallelArrays
type FPA = FloatParallelArray
type PA = ParallelArrays
The Accelerator.ParallelArrays library makes available several overloaded operators for expressing data-parallel array operations as well as functions for creating data-parallel arrays and executing data-parallel computations on targets like GPUs and vector instructions on multicore processors or for the generation of VHDL circuits. Examples of overloaded operators include:
val * : FPA -> FPA -> FPA
val * : float32 -> FPA -> FPA
The first overload for * defines an operation for adding two data-parallel arrays element-wise. The second one defines an operation for multiplying every element of a data-parallel array by a constant.
The Black-Scholes computation makes use of a function to compute a polynomial approximation of the cumulative normal distribution. The CUDA version of Black-Scholes defines this approximation from these equations:
We can compute this polynomial by performing a right fold (called foldBack in F#) using a lambda expression that performs the appropriate multiply and add:
let horner coe k = Array.foldBack (fun a b -> b * k + a) coe 0.0f
The F# language does not allow us to overload literals so we need a slightly different formulation of the polynomial approximation where we locally define a zero array of the appropriate size.
let horner2 coe (k : FPA)
= let zero = new FPA (0.0f, k.Shape)
Array.foldBack (fun a b -> b * k + a) coe zero
The Shape attribute returns the dimensions of an array which is used here to create a new array that has the same dimensions as k but initialized with zeros. The zero array is used as the base case of the fold is never actually constructed during the execution of an Accelerator program because it will be optimized away. Note that the * and + operators here do not refer to any of the standard F# overloads for multiplication and division. Instead, they are overloaded operators that build expression graphs as data structures in the heap that represent data-parallel operations.
The cumulative normal distribution cnd function can be implemented as follows in F# to produce a result which is accurate to within six decimal places using an expansion of a fifth order polynomial:
let cnd (x:float32)
= let coe = [| 0.0f; 0.31938153f; -0.356563782f; 1.781477937f; -1.821255978f;
1.330274429f |]
let l = abs x
let k = 1.0f/(1.0f + 0.2316419f*l)
let poly k = horner coe k
let w = 1.0f - 1.0f/sqrt(2.0f * float32 Math.PI)* exp (-l*l/2.0f) * poly k
if x < 0.0f then
1.0f - w
else
w
Our implementation uses single precision floating point computations so we qualify floating point literals in F# with a `f' character and we also convert the result type of some double precision library functions into single precision by using the float32 type conversion function.
The corresponding Accelerator data-parallel version of cnd follows a similar structure. However. a critical difference is that the Accelerator version works over whole arrays of x and we also introduce an array e which contains the value e in every location as an optimization. Furthermore, we replace the if...then...else statement with a call to Select.
let cndAccel (x : FPA) e
= let coe = [| 0.0f; 0.31938153f; -0.356563782f; 1.781477937f; -1.821255978f;
1.330274429f |]
let l = PA.Abs(x)
let k = 1.0f / (1.0f + 0.2316419f * l)
let poly = horner2 coe k
let w = 1.0f - 1.0f / float32 (Math.Sqrt(2.0 * Math.PI)) *
PA.Pow(e, -l * l / 2.0f) * poly
PA.Select(x, w, 1.0f - w)
The Black-Scholes computation evaluates two expressions: one for an option call and one for an option put.
where S represents the current option price, X is the strike price, T is the time to expiration (in years), r is the continuously compounded risk free interest rate and $v$ is the implied volatility for the underlying stock. A software sequential implementation of these computations can be expressed by the following function which returns a tuple with the call option result in the first element and the put option result in the second element.
let optionCallPut s x t r v
= let d1 = (log (s / x) + (r + v * v / 2.0f) * t) / (v * sqrt t)
let d2 = d1 - v * sqrt t
let expRT = exp (-r * t)
let callOption = s * cnd d1 - x * expRT * cnd d2
let putOption = x * expRT * cnd (-d2) - s * cnd (-d1)
callOption, putOption
The natural logarithm function is not part of the standard Accelerator library so we define it ourselves as:
let loge (x : FPA)
= PA.Log2(x) / PA.Log2(new FPA(float32 Math.E, x.Shape))
Many thanks to Dennis Dzekounoff who spotted an error in my original definition of loge and provided this corrected version.
The Accelerator system currently only support computations that return a single array so we combine the call and option arrays into a single array by padding with zeros and addition. These operations will be optimized into a cheap array append.
// Accelerator 1D computation of the call and put option sharing the computation
// of exp (-r * ts)
let optionCallPutAccel1D (ss : FPA) (xs : FPA) (ts : FPA) r (v : float32)
= let e = new FPA (2.718281828459045f, ss.Shape)
let d1 = loge (ss / xs) + ((r + v * v / 2.0f) * ts) / (v * PA.Sqrt(ts))
let d2 = d1 - v * PA.Sqrt(ts)
let expRT = PA.Pow(e, -r * ts)
let call = ss * cndAccel d1 e - xs * expRT * cndAccel d2 e
let put = xs * expRT * cndAccel (-d2) e - ss * cndAccel (-d1) e
let sRows = ss.Shape.[0]
// We can only return one array as a result so place the put option array
// below the call option array
PA.Pad (call, [|0|], [|sRows|], 0.0f) + PA.Pad (put, [|sRows|], [|0|], 0.0f)
An example of a top-level main program that uses this the GPU (the DX9 target) to compute this function for a small set of four stocks is shown below.
let main(args)
= let dx9Target = new DX9Target()
let s = new FPA ([| 12.3f; 17.2f; 9.6f|])
let x = new FPA ([| 14.2f; 19.5f; 10.4f|])
let t = new FPA ([| 5.6f; 2.5f; 4.7f|])
let putCall = dx9Target.ToArray1D (optionCallPutAccel1D s x t 0.13f 0.25f)
printfn "%A" putCall
0
This program is compiled with the regular F# compiler and linked against the Accelerator library.When the program is run it creates a DX9 GPU target capable of executing Accelerator programs on the users graphics card and then constructs and expression graph for the desired computation which is then shipped to the GPU along with input data for execution. The result array is returned to the main program as a regular F# array which is written out. This is the output produced by compiling and running this main program:
|
To get good performance from Accelerator it is better to work over 2D arrays. The program below is the complete code used to get benchmarking data for the Accelerator DX9 target performance graph in this blog. It runs the Black-Scholes algorithm for input matrices of sizes 500x500, 1000x1000, 1500x1500, . 5000x5000. It runs each test ten times and then reports the average.
open System
open Microsoft.ParallelArrays // Import the Accelerator system
open System.Diagnostics
type FPA = FloatParallelArray // Make abbreviations
type PA = ParallelArrays
// Horner approximation for the Accelerator version
let horner2 coe (k : FPA)
= let zero = new FPA (0.0f, k.Shape)
Array.foldBack (fun a b -> b * k + a) coe zero
// Cumulative normal distribution approximation
let cndAccel (x : FPA) e
= let coe = [| 0.0f; 0.31938153f; -0.356563782f; 1.781477937f; -1.821255978f;
1.330274429f |]
let l = PA.Abs(x)
let k = 1.0f / (1.0f + 0.2316419f * l)
let poly = horner2 coe k
let w = 1.0f - 1.0f / float32 (Math.Sqrt(2.0 * Math.PI)) *
PA.Pow(e, -l * l / 2.0f) * poly
PA.Select(x, w, 1.0f - w)
// Accelerator definition of natural logarithm
let loge (x : FPA)
= PA.Log2(x) / PA.Log2(new FPA(float32 Math.E, x.Shape))
// Accelerator computation of the call and put option sharing the computation of
// exp (-r * ts)
let optionCallPutAccel (ss : FPA) (xs : FPA) (ts : FPA) r (v : float32)
= let e = new FPA (2.718281828459045f, ss.Shape)
let d1 = loge (ss / xs) + ((r + v * v / 2.0f) * ts) / (v * PA.Sqrt(ts))
let d2 = d1 - v * PA.Sqrt(ts)
let expRT = PA.Pow(e, -r * ts)
let call = ss * cndAccel d1 e - xs * expRT * cndAccel d2 e
let put = xs * expRT * cndAccel (-d2) e - ss * cndAccel (-d1) e
let sRows = ss.Shape.[0]
// We can only return one array as a result so place the put option array
// below the call option array
PA.Pad (call, [|0; 0|], [|sRows; 0|], 0.0f) +
PA.Pad (put, [|sRows; 0|], [|0; 0|], 0.0f)
// Create a stop-watch for timing the targets
let sw = new Stopwatch()
let frequency = Stopwatch.Frequency
// A function to execute a given target with a specified input matrix and report
// average running time
let exec2D (target : Target) r v rows cols
= let random = Random (42) // Create some random input arrays
let randomArray rows cols
= Array2D.init rows cols (fun i j -> float32 (random.NextDouble() * 100.0))
let ss = randomArray rows cols
let xs = randomArray rows cols
let ts = randomArray rows cols
let ssA = new FPA (ss) // Create the Accelerator data-parallel arrays
let xsA = new FPA (xs)
let tsA = new FPA (ts)
let iterations = 10 // Run each test ten times
let times
= [for i in 1 .. iterations
do sw.Reset()
sw.Start()
let callputDX9 = target.ToArray2D(optionCallPutAccel ssA xsA tsA r v)
sw.Stop()
let t = double sw.ElapsedTicks / double frequency
yield t
]
printfn "%d\t%d\t%f\n" rows cols (List.sum times / float iterations) // Report average
let r = 0.13f // riskless rate
let v = 0.25f // volatility
[<EntryPoint>]
let main(args)
= printfn "DX9 Black-Scholes benchmark"
let dx9Target = new DX9Target() // Create a GPU target
let dummy = dx9Target.ToArray1D(new FPA([|0.0f|])) // Load DLL
ignore [for size in 0 .. 9 // Run the tests for various sizes of input
do exec2D dx9Target r v (500+size*500) (500+size*500)
]
printfn "[done]"
0
The sequential software version takes 14.1 seconds to compute the call and put results for 16,000,000 stocks running on a machine with one Intel Xeon X5550 processor which contains four cores running at 2.66GHz with 12GB of memory under a 64-bit version of Windows 7 Enterprise. The Accelerator version takes 0.788 seconds when run on my ATI Radeon HD5870 graphics card which represents an 18X speedup. The Accelerator version takes 4.16 seconds when run on all four of the cores using the multicore SSE3 target which represents a 3.4X speedup when using four cores. You can copy and paste the code above into Visual Studio and run it (after installing Accelerator) and see how your own GPU card performs. Please consider sending me your output along with a note specifying which graphics card you used.
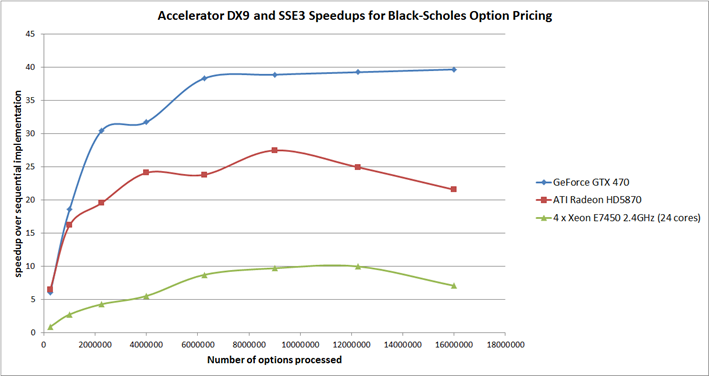
A similar program was written to test out the SSE3 multicore vector target and we also ran the sequential version for each of the 2D input array sizes. The sequential version and the SSE3 multicore vector version were run on a machine with 4 Intel Xeon E7450 cores running at 2.4GHz with 32GB of memory with Windows Server 2008 R2 Enterprise. We used two graphics card to measure speedup: an ATI Radeon HD5870 (it has 1600 stream processing units, 80 texture units and 2GB of memory) and an NVIDIA GeForce GTX 470. The graph below shows for each target the speedup compared to the sequential version of Black-Scholes.
The GeForce GTX 470 can manage around a 40X speedup for an input matrix of size 2500x2500 (i.e. 6,250,000 options) whereas the ATI card achieves around a 25X speedup. Using all 24 processor cores the best speedup we see for the SSE3 vector implementation is around 10X which is due to the fact that not all the operations required by Black-Scholes can be efficiently executed in the SSE3 pipeline. For other examples (e.g. a 2D convolution) we have observed an almost 24X speedup for the SSE3 multicore target.
Given the fairly straight-forward transcription of the sequential program into the corresponding Accelerator version the results achieved show a valuable level of programmer productivity for exploiting the parallel processing capabilities of GPUs and vector instructions running on multiple cores. We do not report results for the FPGA implementation because we have not yet implemented a circuit for computing logarithms. This element-wise calculation is almost certainly memory bound and one would expect even better speedups for computations that work across blocks of the input (e.g. by using the Shift memory transform).
You can download Accelerator from https://research.microsoft.com/en-us/projects/accelerator/default.aspx