An F# Functional Geometry Description of Escher's Fish
This blog explains how Escher's fish wood carving can be expressed in F# using functional geometry which was first presented by Peter Henderson in 1982. This very functional and compositional style of describing pictures is nicely expressed in F#. Functional geometry provides us with a nice algebra for pictures which has been used by the author as the basis of a system for automatically computing the layout of digital circuits expressed in functional languages (e.g. Lava).
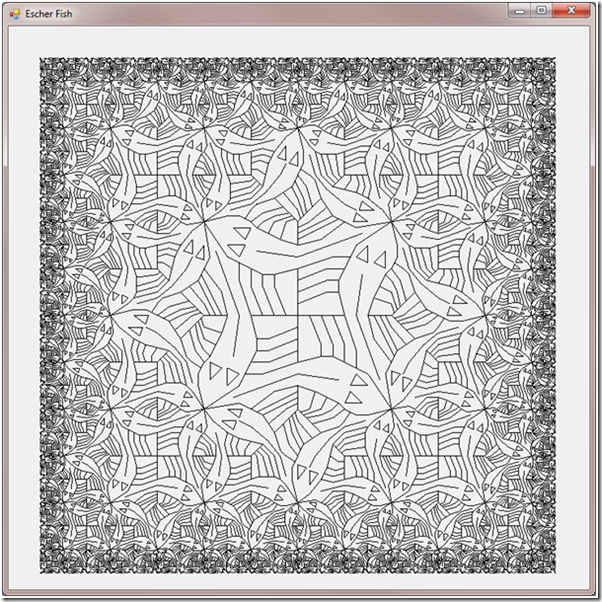
First, here is the picture:
And here are the core F# definitions that are used to make the drawing:
let t = quartet (p, q, r, s)
let side1 = quartet (nil, nil, rot t, t)
let side2 = quartet (side1, side1, rot t, t)
let u = cycle (rot q)
let corner1 = quartet (nil, nil, nil, u)
let corner2 = quartet (corner1, side1, rot side1, u)
let nonet (p1, p2, p3,
p4, p5, p6,
p7, p8, p9)
= above (1.0f, 2.0f, beside (1.0f, 2.0f, p1, beside (1.0f, 1.0f, p2, p3)),
above (1.0f, 1.0f, beside (1.0f, 2.0f, p4, beside (1.0f, 1.0f, p5, p6)),
beside (1.0f, 2.0f, p7, beside (1.0f, 1.0f, p8, p9))))
let corner = nonet (corner2, side2, side2,
rot side2, u, rot t,
rot side2, rot t, rot q)
let squarelimit = cycle corner
The rest of this blog explains how these functions are used to draw the Escher fish picture. A distinctive aspect of drawing pictures using functional geometry is compositional nature in which a composite picture is computed from component pictures by a series of transformations like rotations and scaling operations. In particular there is a lack of concrete coordinates because pictures are typically composed using higher order combinators that work with relative locations e.g. "picture A is to the left of picture B" or "picture A is below picture B".
This picture is produce by transforming four basic tiles called p, q, r and s:
p q r s
The functions used to compute the compute the final drawing operate over a record type that describes points in two dimensions along with some associated members for certain kinds of point operations
type Point = { X : float32; Y : float32 } with
static member (*) (p, a) = {X = a * p.X; Y = a * p.Y}
static member (+) (p1, p2) = {X = p1.X + p2.X; Y = p1.Y + p2.Y}
static member (/) (p, a) = {X = p.X / a; Y = p.Y / a}
static member (~-) p = {X = -p.X; Y = -p.Y}
Note that the ~ symbol is used to specify the overloading of a unary operation (negation in this case). We could define many other overloaded members for *, + etc. but here we define just the operations we need for the functional geometry system. We also use the Point type to describe two-element vectors.
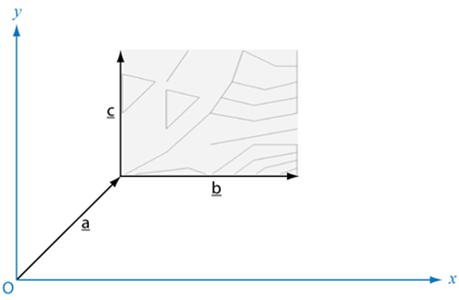
We represent a picture as a function which takes three vectors a, b, and c and produces a drawing with its origin translated by the vector a and with its horizontal and vertical dimensions bounded by the vectors b and c as illustrated below.
A picture is function of the values of the a, b and c vectors which are then used to produce a drawing as a side effect. A picture in our functional geometry system has the type:
type Picture = Point -> Point -> Point -> unit
To draw a line we need a graphics canvas and a pen plus a function plotLine which takes the following parameters:
· m and n which specify the size of the picture grid
· a, b, c which are the vectors which specify the origin and the orientation
· p1 and p2 which specify two Point values which identify the stat and end points of a line segment.
let g = form.CreateGraphics()
let pen = new System.Drawing.Pen(Color.Black)
let plotLine m n a b c (p1, p2)
= g.DrawLine (pen, a.X+b.X*p1.X/m+c.X*p1.Y/n, a.Y+b.Y*p1.X/m+c.Y*p1.Y/n,
a.X+b.X*p2.X/m+c.X*p2.Y/n, a.Y+b.Y*p2.X/m+c.Y*p2.Y/n)
A picture can be expressed as a collection of line segments by using the grid function:
val grid : int * int * (Point * Point) list -> Picture
The grid function is defined as follows:
let grid (m, n, s) a b c
= ignore (List.map (plotLine (float32 m) (float32 n) a b c) s)
This function works by simply applying the plotLine function to each line segment with the appropriate grid size, origin and orientation. The ignore function is used to ensure the return type of this function is unit.
These basic p, q, r and s tiles have little regularity so we define the contents of these tiles by giving their bounding boxes and a list of line segments. Here is the definition of tile p:
let p = grid (16, 16, pointify
[(( 4, 4), ( 6, 0)); (( 0, 3), (3, 4)); (( 3, 4), ( 0, 8));
(( 0, 8), ( 0, 3)); (( 4, 5), ( 7, 6)); (( 7, 6), ( 4, 10));
(( 4, 10), ( 4, 5)); ((11, 0), (10, 4)); ((10, 4), ( 8, 8));
(( 8, 8), ( 4, 13)); (( 4, 13), ( 0, 16)); ((11, 0), (14, 2));
((14, 2), (16, 2)); ((10, 4), (13, 5)); ((13, 5), (16, 4));
(( 9, 6), (12, 7)); ((12, 7), (16, 6)); (( 8, 8), (12, 9));
((12, 9), (16, 8)); (( 8, 12), (16, 10)); (( 0, 16), ( 6, 15));
(( 6, 15), ( 8, 16)); (( 8, 16), (12, 12)); ((12, 12), (16, 12));
((10, 16), (12, 14)); ((12, 14), (16, 13)); ((12, 16), (13, 15));
((13, 15), (16, 14)); ((14, 16), (16, 15));
((16, 0), (16, 8)); ((16, 12), (16, 16))])
The pointfy function is used to convert the list of pairs of integers to pairs containing Points.
let pair2point ((x0, y0), (x1, y1))
= ({X = float32 x0; Y = float32 y0}, {X = float32 x1; Y = float32 y1})
let pointify = List.map pair2point
A useful picture is the empty picture which contains no line segments so we anoint it with a special name:
val nil : Picture
let nil a b c = ()
This picture generating function is more useful than you might think as we shall shortly demonstrate.
A useful higher order function is rot which rotates a picture by 90 degrees.
val rot : Picture -> Picture
let rot p a b c = p (a+b) c (-b)
This is a higher order function because it takes a picture (a function) as its input and returns a picture (a function) as its result. We call such picture to picture functions picture combinators. The application of rot to the tile p is demonstrated below.
p rot p
We will need to place one picture beside another so we define a combinator which performs this task:
val beside : int * int * Picture * Picture -> Picture
let beside (m, n, p, q) (a : Point) (b : Point) (c : Point)
= let lhs = p a (b*m/(m+n)) c
q (a+b*m/(m+n)) (b*n/(m+n)) c
Note that this definition makes use of the overloaded members +, * and - for the type Point. The picture of p beside q is shown below.
Similarly we need to place one picture above another picture:
val above : int * int * Picture * Picture -> Picture
let above (m, n, p, q) (a : Point) (b : Point) (c : Point)
= let top = p (a+c*n/(m+n)) b (c*m/(m+n))
q a b (c*n/(m+n))
We define t to be a quartet formed by placing the four basic riles in a square.
val quartet : Picture * Picture * Picture * Picture -> Picture
let quartet (p1, p2, p3, p4)
= above (1.0f, 1.0f, beside (1.0f, 1.0f, p1, p2),
beside (1.0f, 1.0f, p3, p4))
let t = quartet (p, q, r, s)
Here is the picture of t which shows how nicely the four basic fish tiles fit together:
Another useful picture combinator is cycle which creates a new picture by making successive rotations of an input picture and laying them out using the quartet pattern.
val cycle : Picture -> Picture
let cycle p1 = quartet (p1, rot (rot (rot p1)), rot p1, rot (rot p1))
A picture of cycle (rot t) is shown below.
We now define two pictures which have a very interesting property.
let side1 = quartet (nil, nil, rot t, t)
let side2 = quartet (side1, side1, rot t, t)
side1 side2
The amazing property of the picture t is that when reduced to half its size, it sits perfectly on top of itself (in two different ways)!
We are close to making the final fish picture but first we must define a function that can take nine pictures as its input and produce a regular three by three arrangement.
let nonet (p1, p2, p3,
p4, p5, p6,
p7, p8, p9)
= above (1.0f, 2.0f, beside (1.0f, 2.0f, p1, beside (1.0f, 1.0f, p2, p3)),
above (1.0f, 1.0f, beside (1.0f, 2.0f, p4, beside (1.0f, 1.0f, p5, p6)),
beside (1.0f, 2.0f, p7, beside (1.0f, 1.0f, p8, p9))))
This picture combinator can be used to define a picture called corner.
let corner = nonet (corner2, side2, side2,
rot side2, u, rot t,
rot side2, rot t, rot q)
which is shown below.
The final fish picture, called Square Limit, can now be defined by applying cycle to this corner.
let squarelimit = cycle corner
This produces the picture shown at the top of this blog.
The original deconstruction of Escher's fish was reported by J. L. Locher in 1971 in the book "The World of M. C. Escher". Here we present a "reconstruction" using a nice algebra of picture combinators. For more details about how the fish are drawing using functional geometry look at Henderson's papers e.g. Functional Geometry, or Functional Geometry, or Functional Geometry (yes, they really are all called the same but are somewhat different). The original illustrations for the 1982 paper were done by Mary Sheeran using a functional geometry package implemented in UCSD Pascal. Note that the origin for the drawings on this blog is at the top right hand corner although the origin for the drawings in the original paper is at the bottom right.
Many others have re-implemented Henderson's fish. Here are just a few of them:
· Frank Buss https://www.frank-buss.de/lisp/functional.html
· Bill Clementson https://bc.tech.coop/blog/050213.html
PanBrowser incorporates Conal Elliott's ideas on functional images into an F# library.
I believe the idea behind functional geometry can be applied to description of many sophisticated entities including pictures, circuits and music. In each situation we have to try and understand the underlying structures and look for regular patterns and hierarchy and powerful ways of combining sub-creations into composite creations.
The complete F# program for drawing Escher's fish is shown below which I have tested with F# in Visual Studio 2010 Beta 2.
Satnam Singh
https://research.microsoft.com/~satnams
open System
open System.Windows.Forms
open System.Drawing
type Point = { X : float32; Y : float32 } with
static member (*) (p, a) = {X = a * p.X; Y = a * p.Y}
static member (+) (p1, p2) = {X = p1.X + p2.X; Y = p1.Y + p2.Y}
static member (/) (p, a) = {X = p.X / a; Y = p.Y / a}
static member (~-) p = {X = -p.X; Y = -p.Y}
type Picture = Point -> Point -> Point -> unit
[<EntryPoint>]
let main (args) =
let form = new Form (Text = "Escher Fish", Width = 740, Height = 740, Visible = true)
let g = form.CreateGraphics()
let pen = new System.Drawing.Pen(Color.Black)
let plotLine m n a b c (p1, p2)
= g.DrawLine (pen, a.X+b.X*p1.X/m+c.X*p1.Y/n, a.Y+b.Y*p1.X/m+c.Y*p1.Y/n, a.X+b.X*p2.X/m+c.X*p2.Y/n, a.Y+b.Y*p2.X/m+c.Y*p2.Y/n)
let pair2point ((x0, y0), (x1, y1)) = ({X = float32 x0; Y = float32 y0}, {X = float32 x1; Y = float32 y1})
let pointify = List.map pair2point
let grid (m, n, s) a b c
= ignore (List.map (plotLine (float32 m) (float32 n) a b c) s)
let p = grid (16, 16, pointify
[(( 4, 4), ( 6, 0)); (( 0, 3), (3, 4)); (( 3, 4), ( 0, 8));
(( 0, 8), ( 0, 3)); (( 4, 5), ( 7, 6)); (( 7, 6), ( 4, 10));
(( 4, 10), ( 4, 5)); ((11, 0), (10, 4)); ((10, 4), ( 8, 8));
(( 8, 8), ( 4, 13)); (( 4, 13), ( 0, 16)); ((11, 0), (14, 2));
((14, 2), (16, 2)); ((10, 4), (13, 5)); ((13, 5), (16, 4));
(( 9, 6), (12, 7)); ((12, 7), (16, 6)); (( 8, 8), (12, 9));
((12, 9), (16, 8)); (( 8, 12), (16, 10)); (( 0, 16), ( 6, 15));
(( 6, 15), ( 8, 16)); (( 8, 16), (12, 12)); ((12, 12), (16, 12));
((10, 16), (12, 14)); ((12, 14), (16, 13)); ((12, 16), (13, 15));
((13, 15), (16, 14)); ((14, 16), (16, 15));
((16, 0), (16, 8)); ((16, 12), (16, 16))])
let q = grid (16, 16, pointify
[(( 2, 0), ( 4, 5)); (( 4, 5), ( 4, 7)); (( 4, 0), ( 6, 5));
(( 6, 5), ( 6, 7)); (( 6, 0), ( 8, 5)); (( 8, 5), ( 8, 8));
(( 8, 0), (10, 6)); ((10, 6), (10, 9)); ((10, 0), (14, 11));
((12, 0), (13, 4)); ((13, 4), (16, 8)); ((16, 8), (15, 10));
((15, 10), (16, 16)); ((16, 16), (12, 10)); ((12, 10), ( 6, 7));
(( 6, 7), ( 4, 7)); (( 4, 7), ( 0, 8)); ((13, 0), (16, 6));
((14, 0), (16, 4)); ((15, 0), (16, 2)); (( 0, 10), ( 7, 11));
(( 9, 12), (10, 10)); ((10, 10), (12, 12)); ((12, 12), ( 9, 12));
(( 8, 15), ( 9, 13)); (( 9, 13), (11, 15)); ((11, 15), ( 8, 15));
(( 0, 12), ( 3, 13)); (( 3, 13), ( 7, 15)); (( 7, 15), ( 8, 16));
(( 2, 16), ( 3, 13)); (( 4, 16), ( 5, 14)); (( 6, 16), ( 7, 15));
(( 0, 0), ( 8, 0)); ((12, 0), (16, 0))])
let r = grid (16, 16, pointify
[(( 0, 12), ( 1, 14)); (( 0, 8), ( 2, 12)); (( 0, 4), ( 5, 10));
(( 0, 0), ( 8, 8)); (( 1, 1), ( 4, 0)); (( 2, 2), ( 8, 0));
(( 3, 3), ( 8 , 2)); (( 8, 2), (12, 0)); (( 5, 5), (12, 3));
((12, 3), (16, 0)); (( 0, 16), ( 2, 12)); (( 2, 12), ( 8, 8));
(( 8, 8), (14, 6)); ((14, 6), (16, 4)); (( 6, 16), (11, 10));
((11, 10), (16, 6)); ((11, 16), (12, 12)); ((12, 12), (16, 8));
((12, 12), (16, 16)); ((13, 13), (16, 10)); ((14, 14), (16, 12));
((15, 15), (16, 14))])
let s = grid (16, 16, pointify
[(( 0, 0), ( 4, 2)); (( 4, 2), ( 8, 2)); (( 8, 2), (16, 0));
(( 0, 4), ( 2, 1)); (( 0, 6), ( 7, 4)); (( 0, 8), ( 8, 6));
(( 0, 10), ( 7, 8)); (( 0, 12), ( 7, 10)); (( 0, 14), ( 7, 13));
(( 8, 16), ( 7, 13)); (( 7, 13), ( 7, 8)); (( 7, 8), ( 8, 6));
(( 8, 6), (10, 4)); ((10, 4), (16, 0)); ((10, 16), (11, 10));
((10, 6), (12, 4)); ((12, 4), (12, 7)); ((12, 7), (10, 6));
((13, 7), (15, 5)); ((15, 5), (15, 8)); ((15, 8), (13, 7));
((12, 16), (13, 13)); ((13, 13), (15, 9)); ((15, 9), (16, 8));
((13, 13), (16, 14)); ((14, 11), (16, 12)); ((15, 9), (16, 10))])
let nil a b c = ()
let rot p a b c = p (a+b) c (-b)
let beside (m, n, p, q) (a : Point) (b : Point) (c : Point)
= let lhs = p a (b*m/(m+n)) c
q (a+b*m/(m+n)) (b*n/(m+n)) c
let above (m, n, p, q) (a : Point) (b : Point) (c : Point)
= let top = p (a+c*n/(m+n)) b (c*m/(m+n))
q a b (c*n/(m+n))
let quartet (p1, p2, p3, p4)
= above (1.0f, 1.0f, beside (1.0f, 1.0f, p1, p2),
beside (1.0f, 1.0f, p3, p4))
let t = quartet (p, q, r, s)
let cycle p1 = quartet (p1, rot (rot (rot p1)), rot p1, rot (rot p1))
let side1 = quartet (nil, nil, rot t, t)
let side2 = quartet (side1, side1, rot t, t)
let u = cycle (rot q)
let corner1 = quartet (nil, nil, nil, u)
let corner2 = quartet (corner1, side1, rot side1, u)
let nonet (p1, p2, p3,
p4, p5, p6,
p7, p8, p9)
= above (1.0f, 2.0f, beside (1.0f, 2.0f, p1, beside (1.0f, 1.0f, p2, p3)),
above (1.0f, 1.0f, beside (1.0f, 2.0f, p4, beside (1.0f, 1.0f, p5, p6)),
beside (1.0f, 2.0f, p7, beside (1.0f, 1.0f, p8, p9))))
let corner = nonet (corner2, side2, side2,
rot side2, u, rot t,
rot side2, rot t, rot q)
let squarelimit = cycle corner
let fish = squarelimit {X = 10.0f; Y = 10.0f} {X = 700.0f; Y = 0.0f} { X = 0.0f; Y = 700.0f}
do Application.Run (form)
0