Une première introduction au Deep Learning
Au cours de ce billet, nous, Morgan Funtowicz actuellement en stage au sein de l'équipe et moi-même, vous proposons de découvrir comment fonctionne un des algorithmes aujourd'hui très utilisé dans le monde du Machine Learning ou apprentissage automatique : les réseaux de neurones. Puis, dans un second temps, nous étendrons ces notions au fonctionnement des algorithmes de Deep Learning.
Quelques notions mathématiques simples seront abordées afin de mettre en évidence les points clés des différentes opérations réalisées par ce genre d'algorithme.
Le réseau de neurones
Nous allons débuter notre voyage sur les routes du monde des réseaux de neurones en commençant par définir de quoi il en retourne.
Le Perceptron
Dans sa forme la plus basique, un réseau de neurones ne comporte qu'un seul neurone. Ce neurone peut être représenté comme un système avec n entrées (c.à.d. les variables du modèle) et une sortie. En fait, il y aura autant de sortie(s), que de classe(s) à prédire.
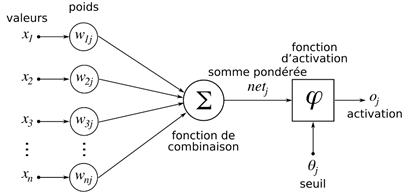
Chacune des n variables d'entrées x va se voir attribuer un poids w lors de la phase d'apprentissage. Ce poids peut être vu comme la force de prédiction de la variable pour le problème :
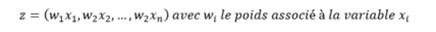
Notre vecteur z, va ensuite passer dans une fonction dite « de combinaison », laquelle prend n variables en entrée, et n'en produit qu'une en sortie. On parle alors de fonction de type « vecteur-à-scalaire » : la somme, la moyenne, la médiane, etc. sont des fonctions de ce type.
Parmi ces fonctions de combinaisons nous pouvons citer :
- Les combinaisons linéaires :
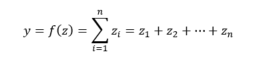
Les combinaisons non-linéaires (notamment de type Gaussienne) :

Enfin, une fois passé dans notre fonction de combinaison, nous nous retrouvons avec une unique valeur (et non plus un vecteur), laquelle va être soumise à une fonction « seuil » :
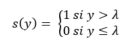
Nous obtenons ainsi un Perceptron, c'est à un dire un réseau de neurones muni d'un seul neurone.
Le réseau de neurones multicouches (MLP ou Multi Layer Perceptron)
Sur la base de la définition précédente de ce qu'était un Perceptron, vous devriez commencer à entrevoir d'où provient le terme de « réseau de neurone ». Un simple Perceptron n'est en fait qu'un classifieur (classifier) linéaire, capable de discriminer uniquement deux classes via une droite - Rappelez-vous la définition de notre fonction de seuil ci-dessus -.
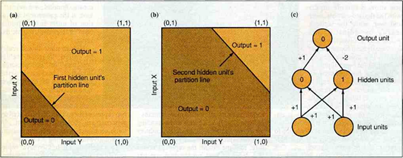
Un exemple simple de problème qu'un Perceptron ne peut pas résoudre, est la fonction XOR (OU Exclusif). En effet, cette fonction n'est pas linéairement séparable (on ne peut pas trouver une droite qui sépare les 0 et les 1).
Question : Soit deux variables x1, x2 pouvant prendre les valeurs 0 ou 1, comment diviser le plan en trouvant une droite séparant les points (0, 0) et (1,1) des points (0, 1) et (1,0) ?
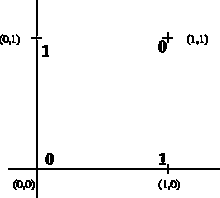
Pour ce faire, il nous faut rajouter une couche cachée, dans le but de diviser le plan en 3 sous-ensembles (modélisés par les droites P1 et P2 sur la figure ci-dessous), soit :
- L'espace inférieur à P1, dont la sortie doit être égale à 0
- L'espace entre P1 et P2, dont la sortie doit être égale à 1
- L'espace supérieur à P2, dont la sortie doit être égale à 0
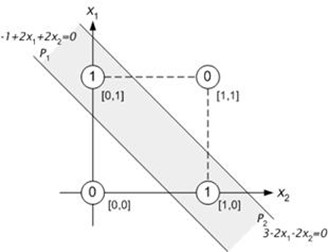
C'est ainsi qu'apparaissent les réseaux dit « multicouches ». Les sorties des Perceptrons de la couche cn sont liées aux entrées des Perceptrons des couches cn+1 :
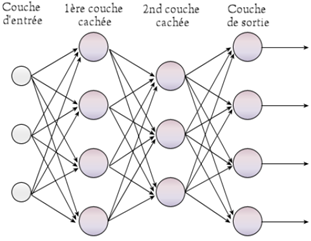
Figure 4 : Représentation graphique d'un réseau de neurones multicouches ( source : Wikipédia )
Ici encore dans ce modèle, chaque connexion entre deux neurones possède un poids. Ces poids sont déterminants dans la prise de décision du modèle ; c'est en effet sur ces derniers que l'algorithme va jouer pour tenter de s'améliorer dans le processus d'apprentissage. On parle alors de « feed-forward » ou de « feedforward ».
Dans la prochaine section, nous allons tenter d'aborder comment sont déterminer ces poids, et ce de manière à être les plus à même à résoudre le problème fourni.
Les couches intermédiaires (entre la couche d'entrée, et celle de sortie), sont appelées couches cachées (hidden layers). Elles permettent d'augmenter la puissance de prédiction du réseau, en combinant plusieurs prédicats.
Revenons à notre exemple de la fonction XOR, insoluble avec un simple Perceptron.
Ajoutons une couche cachée à notre modèle :
|
|
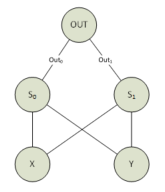
Sur la figure 5, le réseau de gauche présente les pondérations ainsi que les seuils d'activations de chacun des neurones. Sur la droite, la « terminologie », à savoir les noms des variables, pour ce réseau que nous allons reprendre pour la suite de l'explication.
En utilisant une fonction d'activation sigmoïde (dont le seuil est la valeur affichée dans les neurones), nous obtenons la table de résultat suivante :
X |
Y |
Out0 |
Out1 |
OUT |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
Concrètement, notons Out0 la sortie du neurone « à gauche » dans la couche cachée, Out1 la sortie du neurone « à droite » dans la couche cachée et Out0, Out1 les sorties respectives de ces deux couches cachées.
Chaque valeur en entrée du réseau est connectée à chaque neurone dans la couche cachée.
Ainsi, pour tout couple (X, Y) dans {0, 1} nous avons les résultats suivants :
- (0, 0) :
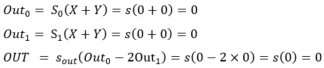
- (0, 1) :
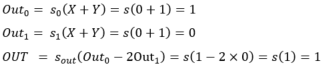
- (1, 0) :
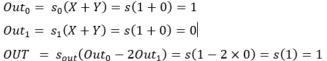
- (1, 1) :
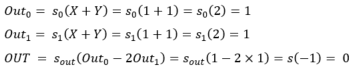
Le contrat est donc rempli, avec une couche cachée comportant 2 neurones, nous avons réussi à représenter un problème non linéairement séparable.
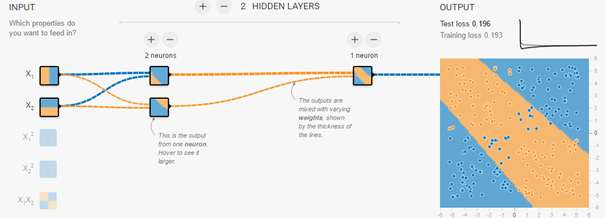
Vous pouvez simuler ce réseau de neurones avec différents outils en ligne comme ici par exemple :
Figure 6 : Simulation d'un réseau de neurones approchant la fonction XOR
A noter que dans la figure 6, la fonction à modéliser n'est pas strictement parlant un XOR, mais s'en rapproche fortement. L'intérêt ici est d'avoir une représentation globale de la manière dont est prise la décision finale, et les interactions entre les différentes couches.
De fait, les deux neurones de la couche cachée servent chacun de séparateur linéaire. L'union des deux permet de définir la bande centrale.
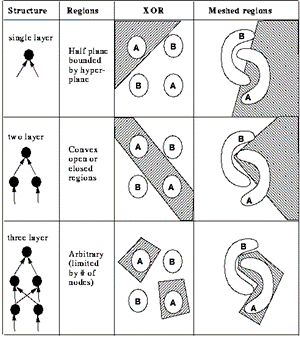
Plus généralement, la topologie de la fonction que l'on souhaite modéliser influe sur celle du réseau de neurones. Une fonction complexe (« accidentée ») nécessitera un nombre de neurones/couches cachées généralement plus important qu'une fonction plus simple.
Sur la figure 7 suivante, vous pouvez comparer la force de prédiction du réseau (colonnes XOR et Meshed Regions), en fonction de la topologie de ce dernier (colonne Structure). Vous pouvez ainsi constater que le nombre de couches, ainsi que le nombre de connexions entre ces couches influent sur la capacité du réseau à modéliser des fonctions plus ou moins complexes.
Mise à jour des différents poids
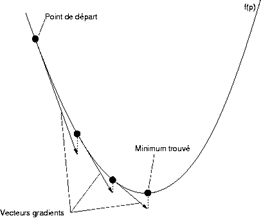
Comme nous l'avons souligné, la valeur définie pour les poids reliant les différents neurones est primordiale pour la précision de l'algorithme. Lors de son apprentissage, le réseau de neurone cherche à résoudre un problème d'optimisation. Dans cette section, nous allons donc voir comment sont mis à jour les différents poids au fur et à mesure de l'apprentissage.
Les poids sont initialisés aléatoirement à l'initialisation du modèle. A chaque itération, l'algorithme va calculer un indicateur de sa performance globale (l'erreur qu'il commet) en comparant la sortie attendue et la sortie prédite :
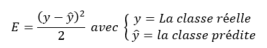
Cette erreur est globale à tout le modèle. Cependant, nous souhaitons mettre à jour les poids wij, en fonction du poids actuel. Pour ce faire, l'algorithme va utiliser une technique appelée « Descente de Gradient », afin d'affiner au fur et à mesure les poids, en fonction de l'erreur commise.
Dans notre cas, cette fonction est définie de la façon suivante :
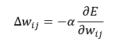
Comment interpréter cette fonction :
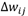 correspond à l'incrément sur la valeur du poids reliant les neurones i et j,
correspond à l'incrément sur la valeur du poids reliant les neurones i et j,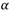 correspond à la valeur du pas d'apprentissage :
correspond à la valeur du pas d'apprentissage :
- Un grand pas d'apprentissage augmentera la probabilité de « sauter » la valeur optimale
- Un pas trop petit nécessitera un grand nombre d'itérations pour trouver la valeur optimale
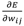 est la variation de l'erreur par rapport au poids entre les neurones i et j.
est la variation de l'erreur par rapport au poids entre les neurones i et j.- Nous cherchons à minimiser l'erreur, donc nous devons décroitre cette fonction
Ainsi les différentes itérations de l'algorithme cherchent à ajuster la valeur des poids entre chaque neurone en fonction de la variation de l'erreur globale.
Le Deep Learning
A présent que nous avons précisé comment fonctionnent les réseaux de neurones de manière générale, nous allons aborder le domaine du Deep Learning.
Cette famille d'algorithmes a permis de faire des progrès importants dans les domaines de la reconnaissance d'images et du traitement du langage par exemple.
Les modèles de Deep Learning sont bâtis sur le même modèle que les perceptrons multicouches précédemment décrits. Cependant, il convient de souligner que les différentes couches intermédiaires sont plus nombreuses.
Chacune des couches intermédiaires va être subdivisée en sous partie, traitant un sous problème, plus simple et fournissant le résultat à la couche suivante, et ainsi de suite. Ainsi, dans le cadre du traitement du langage, imaginons un extrait audio parlant de l'équipe de France de football, les différentes couches pourraient se hiérarchiser de cette façon :
- Couche 1 : Sport.
- Couche 2 : Sport collectif.
- Couche 3 : Football.
- Couche 4 : Equipe de France.
Cette manière d'ordonner les déductions amènent les modèles de Deep Learning à se rapprocher un peu plus du mode de fonctionnement du cerveau humain, en ajoutant au fur et à mesure un contexte de plus en plus précis au sujet sur lequel le modèle opère.
Quelques algorithmes de Deep Learning
Il existe différents algorithmes de Deep Learning. Nous pouvons ainsi citer :
- Les réseaux de neurones profonds (Deep Neural Networks). Ces réseaux sont similaires aux réseaux MLP mais avec plus de couches cachées. L'augmentation du nombre de couches, permet à un réseau de neurones de détecter de légères variations du modèle d'apprentissage, favorisant le sur-apprentissage ou sur-ajustement (« overfitting »).
- Les réseaux de neurones convolutionnels (CNN ou Convolutional Neural Networks). Le problème est divisé en sous parties, et pour chaque partie, un « cluster » de neurones sera créer afin d'étudier cette portion spécifique. Par exemple, pour une image en couleur, il est possible de diviser l'image sur la largeur, la hauteur et la profondeur (les couleurs).
- La machine de Boltzmann profonde (Deep Belief Network) : Ces algorithmes fonctionnent suivant une première phase non supervisée, suivi de l'entrainement classique supervisé. Cette étape d'apprentissage non-supervisée, permet, en outre, de faciliter l'apprentissage supervisé.
Un exemple : CNN (Convolutional Neural Network)
Imaginons que vous présentiez une feuille à une caméra, sur laquelle vous avez écrit un chiffre. Vous aimeriez que l'algorithme derrière la caméra soit capable de déterminer, avec précision, le chiffre que vous avez écrit.
Ce problème peut paraitre simple à traiter, mais il en va différemment pour un ordinateur. Nous allons donc tenter, non pas de lui faire résoudre le problème « quel est ce chiffre ? », mais plutôt de lui faire résoudre « Comment apprendre à reconnaitre un chiffre ? ».
Prenons une image de 28x28 pixels, à savoir le format standard pour le challenge MNIST (Modified National Institute of Standards and Technology) de reconnaissance des chiffres. Cette image est fournie en noir et blanc, avec comme seule inscription un chiffre.
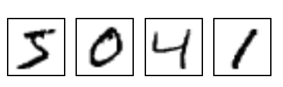
Pour représenter cette image, nous allons utiliser un vecteur binaire de 784 variables (28x28). La ième valeur du vecteur prendra la valeur 0 ou 1 suivant si le ième pixel dans l'image est blanc ou noir.
Un algorithme de Deep Learning va commencer par subdiviser ce problème complexe, en sous problèmes plus simple à résoudre. Pour cela, il va prendre des sous parties de l'image, par exemple, des groupements de pixels de 5x5, 4x4, ou 3x3, et opérer une fonction afin d'extraire des motifs dans cette sous-partie (on parle d'opération de convolution).
Ces fonctions permettent de faire ressortir certaines caractéristiques des images :

Figure 10 : Différents type de filtrages par convolution ( source : UCLA )
Ainsi, différentes transformations sont opérées sur différentes parties de l'image d'entrée, retravaillées puis combinées à la couche suivante, etc., etc. permettant ainsi de générer des cartographies des pixels importants dans l'image.
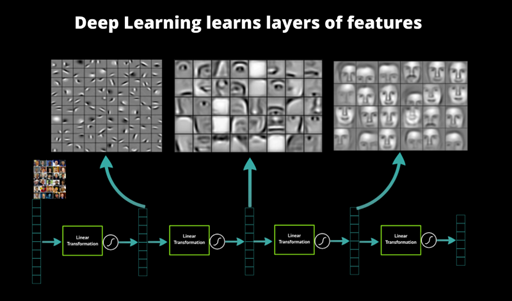
Figure 11 : Vue haut niveau du système de couche d'un CNN ( source : David J. Klein )
L'illustration ci-dessus met en évidence la succession des couches, et l'extraction de l'information qu'elles réalisent. Elle permet aussi de refléter la hiérarchie entre les couches :
- La première se focalise sur une petite portion de l'image (5x5 par exemple).
- La seconde récupère le résultat de toutes les portions précédentes et essaye de repérer de nouveaux indicateurs.
- La troisième va encore plus loin, en suivant le même principe, permettant d'identifier assez précisément les contours du visage.
Vous l'aurez donc compris, chaque couche est génératrice de variables. Chaque couche va venir rajouter son lot de variable issues de la combinaison des précédentes. C'est ici qu'intervient la véritable différence entre un réseau de neurones « classique » et un algorithme de Deep Learning.
Cette faculté à générer des variables, qui plus est, très pertinentes dans un problème donné, permet à l'algorithme de découvrir des indicateurs de « haut niveaux » générant un fort pouvoir prédictif.
En combinant toutes ces informations issues des différentes couches, correctement pondérées, nous obtenons un système capable d'identifier les éléments importants d'une image, dans le but final de prédire la sortie avec la plus forte probabilité d'être correcte.
Des bibliothèques pour accéder plus facilement à ce type de technologies
Les algorithmes de type réseaux de neurones tendent à reproduire le fonctionnement interne du cerveau humain, en tentant de coller aux différentes étapes qui interviennent dans la prise de décision.
Les algorithmes de Deep Learning introduisent la possibilité, en plus du pouvoir prédictif intrinsèque à tout classifieur (classifier), d'auto-générer de l'information pertinente dans le but d'améliorer sa capacité de prédiction, au-delà des capacités observables pour un humain.
De nos jours, ces algorithmes sont encore difficilement utilisables dans la grande majorité des entreprises, du fait des connaissances et de l'architecture nécessaire à la mise en œuvre de tels modèles (notamment de calcul sur puce graphique) qui à l'heure actuelle demeurent encore relativement coûteux.
Cependant, des bibliothèques logicielles commencent à apparaitre ces dernières années, afin de proposer des solutions plus hauts niveaux permettant d'accéder à ce genre de technologies.
Parmi ces bibliothèques, nous pouvons citer en ce qui concerne Microsoft :
- Microsoft Cognitive Services, suite du Project Oxford, auquel nous avions notamment consacré le billet Projet Oxford : la reconnaissance faciale à portée de main et plus encore.
- Microsoft Computational Network ToolKit (CNTK) développé par Microsoft Research.
( Pour les autres acteurs du domaine, citons notamment Google TensorFlow, Nvidia cuDNN et DIGITS, ou encore Facebook Torch. )
Enfin, il est important de souligner que, parmi toutes ces solutions, Microsoft par le biais de Microsoft Cognitive Services permet d'accéder aux possibilités offertes par le Deep Learning, au travers de services/APIs RESTful hébergés dans le Cloud.
Ces services/APIs RESTful couvrent un large panel de cas d'utilisations classiques des algorithmes du Deep Learning, allant de la reconnaissance d'image et de texte, à la compréhension de la voix. Le billet Rendez vos applications plus intelligentes avec les services cognitifs publié dernièrement sur ce même blog revient sur les possibilités offertes par Microsoft Cognitive Services.
Le projet CNTK est quant à lui disponible sur le repo/la forge communautaire GitHub comme notamment annoncé dans les billets Microsoft Releases Open Source Deep Learning Toolkit on GitHub et Microsoft releases CNTK, its open source deep learning toolkit, on GitHub.

Cet outil se présente sous la forme d'une commande, et vous permet de modéliser et d'entrainer des réseaux de neurones de manière parallèle, et éventuellement, distribuée sur plusieurs machines. CNTK fera l'objet d'une série prochaine de billets consacrée au Deep Learning en termes d'illustration de mise en œuvre.