F#: An Array.Parallel Quicksort Implementation
As I mentioned in my previous post, Array.Parallel sort functions demonstrating a Merge Sort using Barrier, I wanted to continue the parallel sort examples with a Quicksort using the Task Parallel Libraries.
F#, as do all functional languages, lend themselves easily to Quicksort implementations. There are many variations of an F# Quicksort, here are a few:
Without continuations:
static member quickSort (list: 'T list) =
let smallThreshold = 16
// Quicksort operation without continuations
let rec quickLoop = function
| [] -> []
| small when small.Length < smallThreshold ->
List.sort small
| p::tail ->
let (lower, upper) = List.partition ((>=) p) tail
List.append (quickLoop lower) (p :: quickLoop upper)
// Perform the sorting
quickLoop list
With continuations, to ensure calls are tail recursive:
static member quickSortCont (list: 'T list) =
let smallThreshold = 16
// Quicksort operation with continuation parameter
let rec quickLoopCont qlist acc =
match qlist with
| [] -> acc []
| small when small.Length < smallThreshold ->
acc (List.sort small)
| p::tail ->
let (lower, upper) = List.partition ((>=) p) tail
quickLoopCont lower (fun loweracc ->
quickLoopCont upper (fun upperacc -> acc (List.append (loweracc) (p :: upperacc))))
// Perform the sorting
quickLoopCont list (fun qlist -> qlist)
The fundamental issue with these implementations is that they are not Quick. The reason for their slowness, for large list/array sorts, is the amount of allocations that need to occur when performing the partitioning; the original list/array is not partitioned/sorted in-place. As an example, to sort a list of 5 Million floats takes just under a minute.
One other issue is that these implementations do not lend themselves to being easily parallelized; there is an implicit dependency on the order of the yield operations. Hence to resolve the sort in-place and parallelize problem we need to tackle several issues:
- Need a recursive loop that will operate on a section (specified range) of an array
- Need a partitioning function that partitions an array in-place, for a specified range
- Once the looping and partitioning functions operate independently on an array partition then parallelism can be introduced
The approach for the Quicksort will be similar to that used for the Merge sort; depending on whether a comparer or projection is specified. If one does not specify a projection the original array is sorted in-place using either a structural comparison or the specified comparer.
If a projection is specified, a separate array is defined for the projected keys. Sorting and comparing is then performed on this keys array. When elements in the array are swapped then both the keys and original array elements are swapped. There is obviously overhead in performing two swaps each time but this is less than calculating the projection for each comparison.
As with the previous sample a full set of sort operations will be demonstrated using the Quicksort; namely:
module Array =
module Parallel =
let sort (array: 'T []) =
ParallelQuickSort.Sort(array)
let sortBy (projection: 'T -> 'Key) (array: 'T []) =
ParallelQuickSort.SortBy(array, projection)
let sortWith (comparer: 'T -> 'T -> int) (array: 'T []) =
ParallelQuickSort.SortWith(array, comparer)
let sortInPlace (array: 'T []) =
ParallelQuickSort.SortInPlace(array)
let sortInPlaceBy (projection: 'T -> 'Key) (array: 'T []) =
ParallelQuickSort.SortInPlaceBy(array, projection)
let sortInPlaceWith (comparer: 'T -> 'T -> int) (array: 'T []) =
ParallelQuickSort.SortInPlaceWith(array, comparer)
So once again here is the full code listing:
type ParallelQuickSort() =
static member public Sort(array: 'T []) =
let arraySort = Array.copy array
ParallelQuickSort.SortInPlaceInternal(arraySort)
arraySort
static member public SortBy(array: 'T [], projection: 'T -> 'Key) =
let arraySort = Array.copy array
ParallelQuickSort.SortInPlaceInternal(array, projection = projection)
arraySort
static member public SortWith(array: 'T [], comparer: 'T -> 'T -> int) =
let arraySort = Array.copy array
ParallelQuickSort.SortInPlaceInternal(array, comparer = comparer)
arraySort
static member public SortInPlace(array: 'T []) =
ParallelQuickSort.SortInPlaceInternal(array)
static member public SortInPlaceBy(array: 'T [], projection: 'T -> 'Key) =
ParallelQuickSort.SortInPlaceInternal(array, projection = projection)
static member public SortInPlaceWith(array: 'T [], comparer: 'T -> 'T -> int) =
ParallelQuickSort.SortInPlaceInternal(array, comparer = comparer)
// counter for the degree of paallism
static member private CurrentDop = ref 0
static member private TargetDop = Environment.ProcessorCount * 2
// Private function that is used to control the sorting
static member private SortInPlaceInternal(array: 'T [], ?comparer: 'T -> 'T -> int, ?projection: 'T -> 'Key) =
// definition of runtime parameters
let smallThreshold = 32
let parallelThreshold = 4 * 1024
// define a key array if needed for sorting on a projection
let keys =
match projection with
| None -> [||]
| Some p -> Array.Parallel.init array.Length (fun idx -> p array.[idx])
// used to do the partition and sort comparisions
let sortComparer =
match comparer with
| None -> ComparisonIdentity.Structural<'T>
| Some c -> ComparisonIdentity.FromFunction c
let projectionComparer =
ComparisonIdentity.Structural<'Key>
// swap elements (and maybe keys)
let inline comparerResult left right =
match projection with
| None -> sortComparer.Compare(array.[left], array.[right])
| Some _ -> projectionComparer.Compare(keys.[left], keys.[right])
let inline swap x y =
match projection with
| None ->
let ae = array.[x]
array.[x] <- array.[y]
array.[y] <- ae
| Some _ ->
let ae = array.[x]
array.[x] <- array.[y]
array.[y] <- ae
let ak = keys.[x]
keys.[x] <- keys.[y]
keys.[y] <- ak
// sort three elements
let inline sortThree low middle high =
if (comparerResult middle low < 0) then
swap middle low
if (comparerResult high middle < 0) then
swap high middle
if (comparerResult middle low < 0) then
swap middle low
// perform an in place partition with pivot in position low
// taking average of 3 rather than -> swap low pivot
let inline partition (low:int) (high:int) =
let pivot = (low + high) / 2
sortThree pivot low high
let mutable last = low
for current in (low + 1)..high do
if (comparerResult current low < 0) then
last <- last + 1
swap last current
swap low last
last
// define the sort operation using Parallel.Invoke for a count
let rec quickSortCount (low:int) (high:int) =
let sortLen = high - low + 1
match sortLen with
| 0 | 1 -> ()
| 2 -> if (comparerResult high low < 0) then swap high low
| small when small < smallThreshold ->
match (comparer, projection) with
| (Some _, _) -> Array.Sort(array, low, sortLen, sortComparer)
| (_, Some p) -> Array.Sort(keys, array, low, sortLen)
| (_, _) -> Array.Sort(array, low, sortLen)
| _ ->
let pivot = partition low high
if (!ParallelQuickSort.CurrentDop < ParallelQuickSort.TargetDop && sortLen > parallelThreshold) then
Interlocked.Increment(ParallelQuickSort.CurrentDop) |> ignore
Parallel.Invoke (
Action(fun () -> quickSortCount low (pivot - 1)),
Action(fun () -> quickSortCount (pivot + 1) high))
Interlocked.Decrement(ParallelQuickSort.CurrentDop) |> ignore
else
quickSortCount low (pivot - 1)
quickSortCount (pivot + 1) high
// Perform the sorting
quickSortCount 0 (array.Length - 1)
So a few notes about the code.
You will notice that all the secondary functions are marked as inline. This means that all these functions are integrated into the calling code; needed to ensure the code is performant.
The comparerResult function is the one that compares array elements. As mentioned, depending on whether a projection has been specified, this compares elements from the original array or the keys array. Similarly the swap function swaps elements from the keys array only if a projection has been specified.
The partitioning for this sort takes the approach of using the median of the first, middle, and last elements in the array. The median value is then moved into the first position, low index, and the remainder of the elements are then partitioned based on this first value.
The actual partitioning is performed using a simple for loop. The rational for this rather than something like Seq.fold (where the accumulator is the last index moved) is once again purely performance.
When performing the recursive sort, as most Quicksort implementations do, when the array size drops below a certain threshold a normal array sort is performed; the sort type usually being an Insertion sort.
The last,and probably most important, thing to consider was how best to parallelize the recursive call. Options for this are discussed by Stephen Toub in his whitepaper “Patterns for Parallel Programming: Understanding and Applying Parallel Patterns with the .NET Framework 4”; well worth a read if you haven't already done so.
This code uses the approach that parallelism is invoked only if the array size is greater than a threshold size (as parallel invocations incur cost) and the current degree of parallelism is below a certain threshold (if all cores are busy default to serial invocation). To support this, the following type definitions are used:
static member private CurrentDop = ref 0
static member private TargetDop = Environment.ProcessorCount * 2
Having the CurrentDop defined as static means that if multiple sorts are in flight within the same process the system will not get overloaded with sorting threads.
The alternative approach, again as mentioned by Stephen, is to parallelise to a certain recursive depth after which, when the number of threads is up to the number of cores (log2 of the cores), one defaults to the normal serial behaviour:
let rec quickSortDepth (low:int) (high:int) (depth:int) =
let sortLen = high - low + 1
match sortLen with
| 0 | 1 -> ()
| 2 -> if (comparerResult high low < 0) then swap high low
| small when small < smallThreshold ->
match (comparer, projection) with
| (Some _, _) -> Array.Sort(array, low, sortLen, sortComparer)
| (_, Some p) -> Array.Sort(keys, array, low, sortLen)
| (_, _) -> Array.Sort(array, low, sortLen)
| _ ->
let pivot = partition low high
if (depth > 0 && sortLen > parallelThreshold) then
Parallel.Invoke (
Action(fun () -> quickSortDepth low (pivot - 1) (depth - 1)),
Action(fun () -> quickSortDepth (pivot + 1) high (depth - 1)))
else
quickSortDepth low (pivot - 1) 0
quickSortDepth (pivot + 1) high 0
let targetDepth = int (Math.Log(float Environment.ProcessorCount, 2.0)) + 1
quickSortDepth 0 (array.Length - 1) targetDepth
As Stephen noted in his paper the issue with this approach are unbalanced partitions affecting the parallelism.
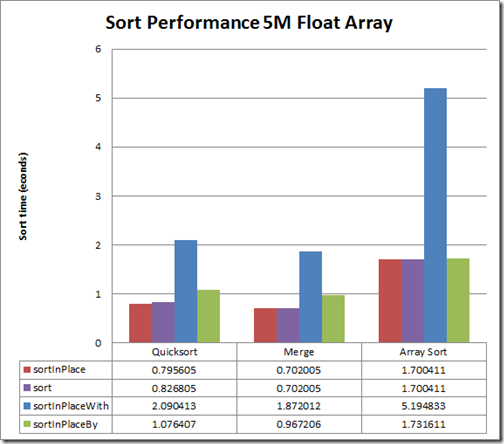
So how does this all perform? Surprisingly, the original Merge sort is a little faster. Using my quad-core laptop with an array of 5 million floats the numbers are (the projection is defined as (sqrt << abs)):
One final metric worth mentioning is that if one creates a comparer from the projection and then performs a sortInPlaceWith then the Quicksort takes about 3 seconds. This is compared with the sortInPlaceBy of about 1 second.
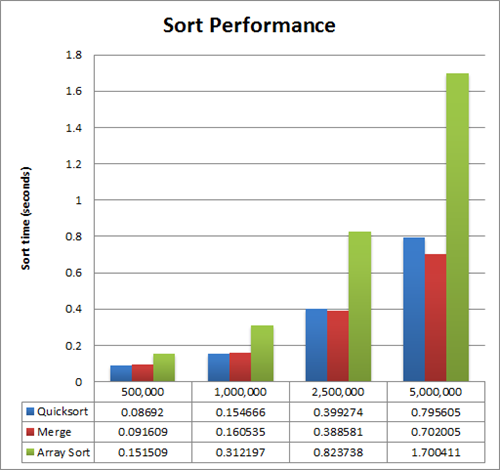
The Quicksort however is faster for smaller arrays (up to 2 Million floats); here is a summary for the sortInPlace operation:
Thus looking at these numbers one may decide to perform a merge sort when the array size exceeds 2 million. In addition at around 50,000 elements you will find that the base sort routines are more performant than a Quicksort. Thus one may define the Parallel.Array extension as follows:
module Array =
module Parallel =
let smallThreshold = 48 * 1024
let largeThreshold = 2048 * 1024
let sort (array: 'T []) =
match array.Length with
| length when length > largeThreshold -> ParallelMergeSort.Sort(array)
| length when length > smallThreshold -> ParallelQuickSort.Sort(array)
| _ -> Array.sort array
let sortBy (projection: 'T -> 'Key) (array: 'T []) =
match array.Length with
| length when length > largeThreshold -> ParallelMergeSort.SortBy(array, projection)
| length when length > smallThreshold -> ParallelQuickSort.SortBy(array, projection)
| _ -> Array.sortBy projection array
let sortWith (comparer: 'T -> 'T -> int) (array: 'T []) =
match array.Length with
| length when length > largeThreshold -> ParallelMergeSort.SortWith(array, comparer)
| length when length > smallThreshold -> ParallelQuickSort.SortWith(array, comparer)
| _ -> Array.sortWith comparer array
let sortInPlace (array: 'T []) =
match array.Length with
| length when length > largeThreshold -> ParallelMergeSort.SortInPlace(array)
| length when length > smallThreshold -> ParallelQuickSort.SortInPlace(array)
| _ -> Array.sortInPlace array
let sortInPlaceBy (projection: 'T -> 'Key) (array: 'T []) =
match array.Length with
| length when length > largeThreshold -> ParallelMergeSort.SortInPlaceBy(array, projection)
| length when length > smallThreshold -> ParallelQuickSort.SortInPlaceBy(array, projection)
| _ -> Array.sortInPlaceBy projection array
let sortInPlaceWith (comparer: 'T -> 'T -> int) (array: 'T []) =
match array.Length with
| length when length > largeThreshold -> ParallelMergeSort.SortInPlaceWith(array, comparer)
| length when length > smallThreshold -> ParallelQuickSort.SortInPlaceWith(array, comparer)
| _ -> Array.sortInPlaceWith comparer array
As always hope you find this code useful.
Written by Carl Nolan