Volume in Windows Vista, part 1: What is "volume"?
I've avoided writing about this because it's "complicated", but people are starting to ask questions that indicate that they're confused so here goes. It's going to take several posts to cover this, so please bear with me.
So what IS volume, anyway?
Simply stated, volume is a measurement of the “loudness” of a sound (to a physicist or audio engineer, the answer is MUCH more complicated than that). There are lots of ways you can calculate volume, one measurement is in decibels (dB), which is a measure of the sound pressure level (SPL) emitted by a speaker.
In general, when discussing volume, there are two terms typically used – attenuation and gain. Attenuation represents a reduction in the amplitude of an audio signal, gain represents an amplification of that signal. If you look at a pro audio receiver, you’ll notice that the receiver represents its loudness as a negative number of decibels (-20dB, for example). This indicates that the receiver is attenuating the input signal by 20dB. By tradition, attenuation is measured in negative decibels, amplification is measured in positive decibels.
Audio signals flow through an electrical path and at different points in the path, there are opportunities to either amplify or attenuate the signal – the locations at which the amplification or attenuation occur are called “gain stages”, and they can occur in either analog or digital signals (an amplifier represents a gain stage, as does a potentiometer).
How does volume relate to digital audio?
When converting an analog signal to digital, the analog signal is sampled – the system measures the amplitude of the signal with fairly high resolution (44,100 samples per second for CD audio), then converts the samples to a digital value (a 16 bit integer for CD, or potentially a 32bit floating point value). In both cases, there is a reference range of legal samples – for this example, let’s assume that values range from -1.0 to 1.0 (it makes things easier).
Consider the following waveform:
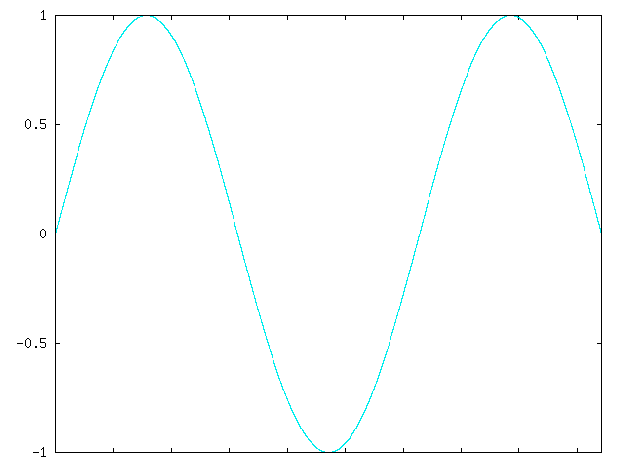
When the sample is digitized, it is converted to individual samples like below:
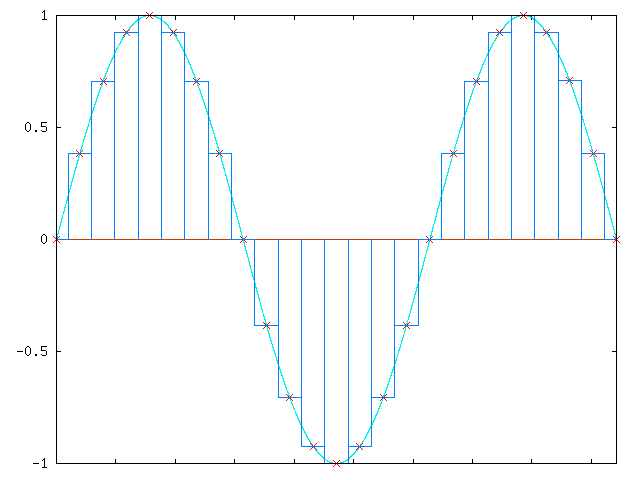
Attenuation simply reduces the amplitude of the digital samples, and amplification simply increases the value of the signals.
For the reference sample, if you attenuate the sample by 50%, you get something like this:
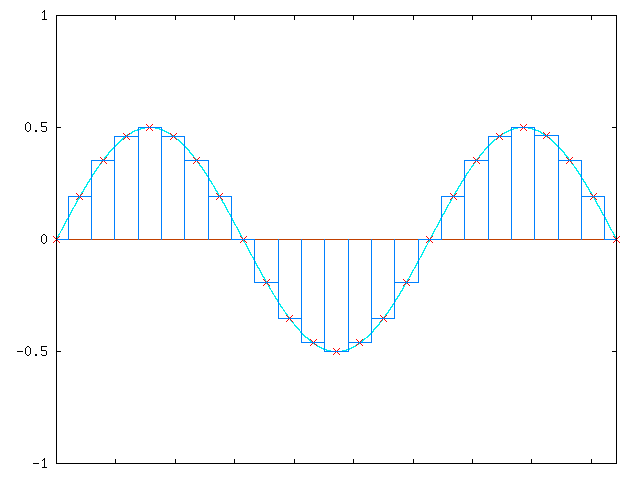
Note that the waveform hasn’t changed shape, it’s just smaller.
If, on the other hand, if you amplify the same signal by 50%, you get:
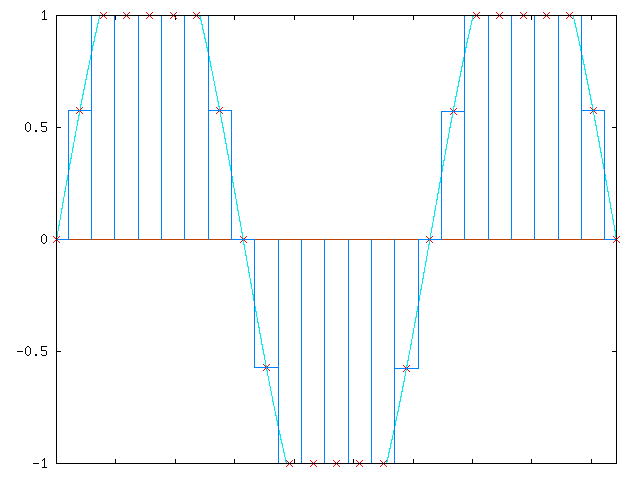
Note that the samples that went beyond the +1 and -1 range were “clipped” – the samples can’t be represented digitally, so they were cut off. This clipping is very bad, and causes significant audio distortions. The new waveform doesn't really reflect the original waveform.
In addition, if a fixed point digital signal is attenuated then later digitally amplified, the signal resolution will be degraded – if, for example you apply a -6dB attenuation (which reduces the volume by 50%), you divide each of the samples in half (32767 becomes 16383). If you later amplify the signal digitally, you get 32766 – and thus you’ve lost some of the original signal information.
If, on the other hand, you’re using a floating point digital signal, you can attenuate and amplify with less worry – if you apply the same -6dB attenuation and amplification to a floating point sample, the division and multiplication cancel out (.75 becomes 0.375, becomes .75).
This is a large part of the reason the audio pipeline was converted to floating point in Vista – a floating point pipeline allows significantly more resolution and higher accuracy when manipulating the digital samples.
Btw, this loss of fidelity doesn’t happen when amplifying analog signals. That’s why it’s important that any amplification be done using analog signals, not digital signals – digital amplification is always lossy.
For audio hardware in Windows, the audio driver specification requires that for all hardware volume controls on the system that 0dB represent a full fidelity pass-through of audio samples – audio hardware can support either amplification or attenuation (or neither), but 0dB always represents “don’t change the samples”.
Please note that some audio hardware on the market does NOT follow this recommendation. We’ve seen audio devices that support a volume range of +0dB to +96dB. We’ve also seen devices that support volume ranges of +10dB to +60dB (mostly these are microphones).
Ok, so much for the basics on "volume", tomorrow I'll start discussing how volume works in the audio engine on Vista.