Representing dependencies in code
It is more often than you would suspect that people have to deal with some sort of dependencies in an application they're developing. In this post I'll talk about some common algorithms and data-structures to work with dependencies that might turn out helpful with some real-life programming tasks.
To better understand what kind of dependencies I'm talking about, let's consider a couple of examples first.
Example 1: A Spreadsheet Application
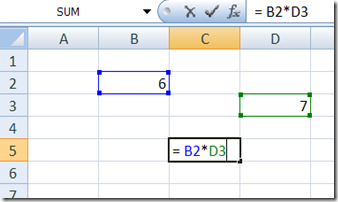
In Excel every cell can contain a formula which depends on other cells:
Here we have the value in C5 depending on values in B2 and D3. A couple of things to note:
- Whenever a value in B2 changes, the value in C5 is recalculated automatically based on the formula.
- A cell can have multiple dependencies (i.e. cells that this cell depends upon)
- Cells can build dependency chains and trees (whenever a cell is changed, the entire subtree is recalculated)
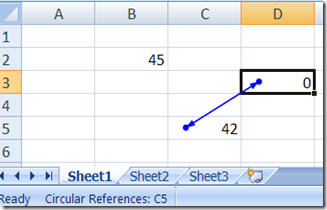
- Cells cannot have circular dependencies. If you try to create a circular dependency, Excel will show a message box and draw a nice blue arrow to indicate a cycle in the dependency graph:
Example 2: Visual Studio Project System
If you look at a solution in Visual Studio with multiple projects, those projects will most probably reference other projects. When you build the solution, Visual Studio somehow figures out the correct order in which to build the projects, and always guarantees that all the dependencies are built before it builds any given projects.
Same things to note here:
- Whenever a project changes, VS figures out that its dependent projects will need to be rebuilt during the next build.
- A project can reference multiple projects
- Projects can build dependency chains and trees
- Projects cannot have circular references.
Example 3: Dynamic Geometry
In a dynamic geometry application, like the one I'm building as a hobby project, geometric figures depend on other figures during their construction. For instance, you need two points to draw a line - and this line will depend on the two points.
- As you move a point, the line will redraw to pass through this point
- A figure can depend on multiple figures (a parallel line needs a point and a line to be constructed)
- Same as above
- Same as above
Why is this important?
It is important to be aware of such things as dependencies in your domain model and to be explicit about them in your code. Clearly expressed intent in code is goodness that is incredibly useful for those who write the code, who read the code and who use the code.
I've seen a case where a program naively relied on the order in which objects were created, and failed to save them if the order was changed. It gave a message box like "Please rearrange your objects because I can't figure out in which order to save them, because they have complex interdependencies". Well, the dependency scheme was exactly like in the three examples above, so the application could very well handle the dependencies itself.
Can you imagine Visual Studio giving you a message box saying: "Please rearrange the projects in your solution because I can't figure out in what order to build them"? That's why it's important - thinking a little bit about such things can make your code clean, smart, robust and the application easy to use.
Data structure: DAG (Directed Acyclic Graph)
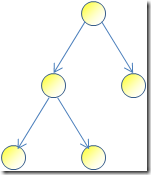
A data structure that is commonly used to model such dependencies is called DAG. Wikipedia does a great job describing it, so I will just highlight some points here. First, and foremost, every tree is a DAG:
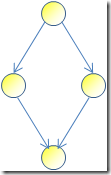
But in a tree, a node cannot depend on more than one parent (like single inheritance in C#). In a DAG, a node can very well have more than one parent:
This "diamond" shape is well known to C++ programmers - multiple inheritance is a great example of a DAG. Wikipedia makes a great point that a DAG "flows" in one direction (there can be no cycles).
Each node in a DAG has a list of dependencies ("parents") and a list of dependents ("children"):
interface IDagNode
{
IDagNodeList Dependencies { get; }
IDagNodeList Dependents { get; }
}
You don't have to store Dependents as well and recalculate them every time, but storing dependents greatly simplifies many algorithms, and it also makes the data structure symmetric.
With a tree, you clearly know where's the top (root) and the bottom (leaves). A DAG, on the other hand, is symmetric - it can have many "roots" and many "leaves". Our diamond, for example, has one root (above) and one leaf (below) - but if you draw the arrows in the opposite direction, a root becomes a leaf, and a leaf becomes a root. Officially, a "root" is called a source, and a "leaf" is called a sink.
Let's try to give some definitions:
- Node A directly depends on node B if A.Dependencies.Contains(B).
- Node A depends on node B if A directly depends on B or A directly depends on some C, which in turn depends on B (recursive definition).
- A node is a source if it doesn't depend on any other node.
- A node is a sink if no other node depends on it.
Note that a non-empty DAG always has at least one source and at least one sink. Finding sources and sinks is easy - iterate over all nodes and select those that have their Dependencies/Dependents collection empty.
Algorithm: Topological Sort
So what's the use of a data structure if we don't have a useful algorithm that comes with it? Well, it turns out, we do. Every DAG can be linearized (serialized) into a sequence, where a node only depends on nodes that come before it. This special sequence is called topological sort of the DAG.
Thus, to figure out the build order in which we want our Visual Studio projects to be built, we just take all of our projects and sort them topologically with regard to their references.
The algorithm is actually pretty simple:
- Before visiting a note, check if we have already visited it (e.g. using a hashtable or marking the node) - don't visit it the second time.
- For every node that we visit, first visit all the dependencies recursively.
- After visiting the children, append the node being visited to the end of the results list.
After visiting all the nodes, the results list will contain all the nodes sorted topologically.
In my plane geometry application I use topological sorting to recalculate the coordinates of figures in the correct order - if I recalculate a line before a point is moved, the line will use the points old coordinates and will appear off-base. If you're interested, here's the source code.
The problem with my implementation is that the algorithm is too tied to the nature of the objects being sorted (figures). In the future, I'll look into making this algorithm generic and reusable in other projects.
Finally, I'll be interested in any examples of DAGs that you come across. I'm collecting such examples, so I'll be grateful if you tell me about your experiences with DAGs and topological sorting and where you encountered this remarkable data structure.