Solving My Pocket Solitaire using Bottom-Up method
This post continues My Pocket Solitaire series.
In my previous post I went through how to solve this puzzle using top-down approach. However as I explained it’s quite inefficient way to just “brute force” the tree from Top-Down and try to get possible solutions.
So what if we would like to know that how many unique solutions there are in this puzzle? Getting solution for that question using Top-Down method would take very long time… therefore we need other ways to answer that question. This brings us to Bottom-Up method which is pretty good fit for this kind of problem. More about Top-Down and Bottom-Up design in Wikipedia.
Idea of bottom-up solving starts from the core idea that since we know the desired target state of the board (a.k.a. end state) then we can use that information to remove a lot of unwanted board states during processing. If you compare this to Top-Down then you don’t actually know that does this certain selected tree path ever lead to target board state. And since you have to process the tree to last possible state before you can say that did we reach the target state or no… you’ll do a lot of unnecessary work. And in simple terms…. if you do a lot of unnecessary work you end up being slow and vise versa ![]() . In Bottom-Up method we can remove a lot of unnecessary work because we *know* that we’re starting from *valid* end position and all the paths to the root contribute to the final solution count.
. In Bottom-Up method we can remove a lot of unnecessary work because we *know* that we’re starting from *valid* end position and all the paths to the root contribute to the final solution count.
Of course there is downside in this solution => This is more complex solution than the standard Top-Down approach. So if you want to use this kind of algorithms in your own applications then you need to pay more attention when implementing it. Next I’ll try to describe Bottom-Up approach so that it would make sense to you. Here’s the Pseudocode of it:
Initialize list of previous board states with target state of board
Initialize list of board states to empty
Loop 31 times
Clear list of board states
For each board state in list of previous board states
Restore board state to current board state
Get list of valid backward moves from this current board state
For each move in valid backward moves list
Make backward move from this current board state
Store new board state to list of board states
Aggegate all board states in the list of board states
Set list of previous board states to be list of board states
End result is at the list of previous board states
First we have create lists where we store information about board states that the algorithm is currently working on. Then we start loop which we’ll repeat 31 times (depth of the solution tree ![]() ). Inside that loop we’ll restore previously stored board state. Then we’ll do all the possible backward moves from that board state so that we get new board states but all of them are one level up in the solution tree (and thus the Bottom-Up naming). Since we’re restoring one-by-one all the previously stored board states and then getting all board states of one level up from those we’ll might be getting duplicate board states at the end. Therefore we need to “aggregate” (or “group”) those duplicates away. And when we have repeated this logic for 31 times we’ll be having list with 5 items which describe the board state where all the paths led to. You might be wondering that how come 5 items in the list since only 1 would be correct answer but I’ll answer that later.
). Inside that loop we’ll restore previously stored board state. Then we’ll do all the possible backward moves from that board state so that we get new board states but all of them are one level up in the solution tree (and thus the Bottom-Up naming). Since we’re restoring one-by-one all the previously stored board states and then getting all board states of one level up from those we’ll might be getting duplicate board states at the end. Therefore we need to “aggregate” (or “group”) those duplicates away. And when we have repeated this logic for 31 times we’ll be having list with 5 items which describe the board state where all the paths led to. You might be wondering that how come 5 items in the list since only 1 would be correct answer but I’ll answer that later.
Let’s walkthrough the implementation step-by-step. So first we set the board to end state:
From this end state we have to get valid backward moves. Valid moves are highlighted in the above image with red arrows.
Next we try to remove duplicates board states but there isn’t yet duplicates in this first round. Then we’ll store these 4 board states to list and continue with next iteration of the loop. Again we’ll get valid backward moves but this time we have to repeat the process for all 4 board states that we have stored earlier. This will give us then 12 new board states in this iteration (see previous post which has table and graph about the growing ratio). And again there are no duplicates in this round so we can continue to next iteration. which gives us 60 new board states and no duplicates. However next iteration is interesting since we’ll get 400 new board states but when we get rid of the duplicates we will be left with only 296 new board states. This means that there are quite many paths that lead to exactly same board state. And since we’re now focusing to answer the question that “how many unique solutions there are in this puzzle” we can safely get rid of the duplicates. And if you can get rid of 100+ unnecessary calculations in one level you can just imagine what this does to performance in the long run! But of course we cannot just blindly remove duplicates because that would lead to wrong end result. We have to aggregate those solution counts together before we ignore the duplicate. This just means that if two paths come together then you have to make sure that you count them together that you know how many times you can end up to the final position from this particular position.
Then we’ll just keep repeating above formula until we’re left to the last position on the board. Maybe surprisingly there are suddenly five board positions still left. One of them is the real solution where the last missing piece is really in the middle of board. Other four solutions are marked with yellow color:
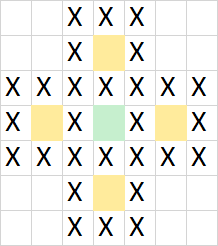
Magic number
And this solution with the green color will give us magical number of 40861647040079968 (formatted: 40’861’647’040’079’968). That is so large number that Excel displays it like this: 4.086E+16. So you can say that this game has 40 petasolutions! Similarly you end up to these yellow (from above picture) start positions and they have each 10215411760019992 solutions (I mean that if you would start from that position you would end up to final position with this many different routes). If you them sum up these four yellow start up position solutions then it will lead again to same magic number 40861647040079968 ![]() .
.
How long does it take to calculate this?
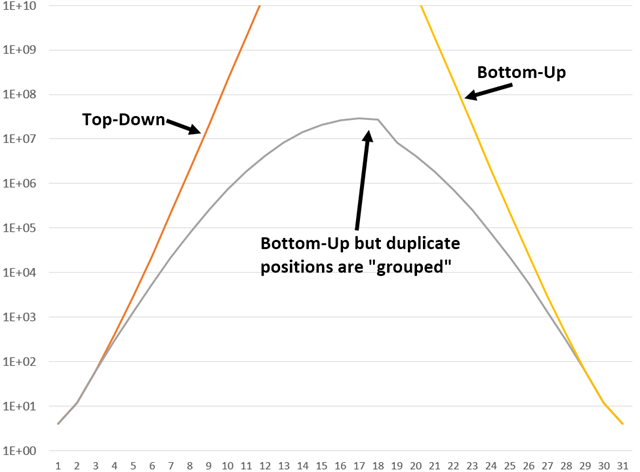
If you want to compare this to the Top-Down approach (or Bottom-Up but without “grouping” of similar board positions) then I think below picture tells it all. X-axis is the depth of the tree in processing and Y-axis is the number of board positions:
From that it’s quite easy to see that you optimize the performance a lot because you can eliminate duplicate board positions away and thus don’t waste any energy on processing them.
I have implemented this Algorithm in C++ using different mechanisms such as:
- Single thread
- Multithread
- Parallel Patterns Library (PPL)
- Mapper-Reducer – Multiple processes (more about this in future posts)
Multithread approach takes on my laptop 1,5 hours! This is not bad if you take into consideration complexity of the given task.
Hopefully you got an idea how you could use Bottom-Up method to solve some tough problems. In future posts I’ll open up more different implementations such as mapper-reducer etc.
Anyways... Happy hacking!
J