Making ParallaxUi look right - field of view selection
In my last post, I said that "one of the more subtle aspects of the otherwise pretty straightforward ParallaxUi is the ‘registration' between the 2D and the 3D", and proceeded to discuss how this is done. This amounted to figuring out how far back to place our camera based on a given Field of View (FOV).
The other subtle aspect of ParallaxUi is how we actually choose that FOV for the camera. It's not as simple as just choosing a single FOV to use throughout all interactions.
We know from experience that when a camera is close to a set of subjects, the depth differences between those subjects is much more apparent than when the camera is far away from the subjects. And when the camera is at infinity, everything appears to be in the same plane.
In order to achieve the parallax effect that ParallaxUi demonstrates, and be able to experience these objects in 3D, the camera needs to be reasonably close to the objects. However, when the camera is close, it accentuates the depth differences between the objects. Thus, if ParallaxUi maintained a constant camera distance, the initial view, when we rotated even slightly away from the 2D representation, would jump dramatically and introduce unwanted depth effects.
Here's an example. This first image is a head on view of our sample UI:
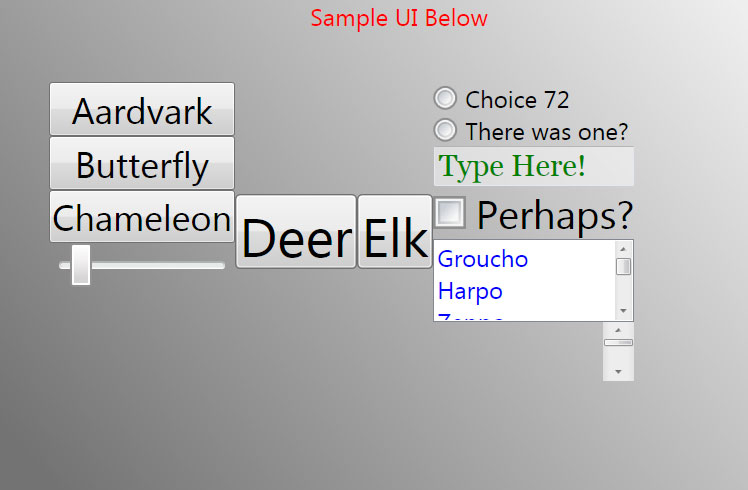
This next image is from a broken version of the code that always keeps the camera at the same distance, and it's taken when the sample UI is rotated just slightly off of 0°:
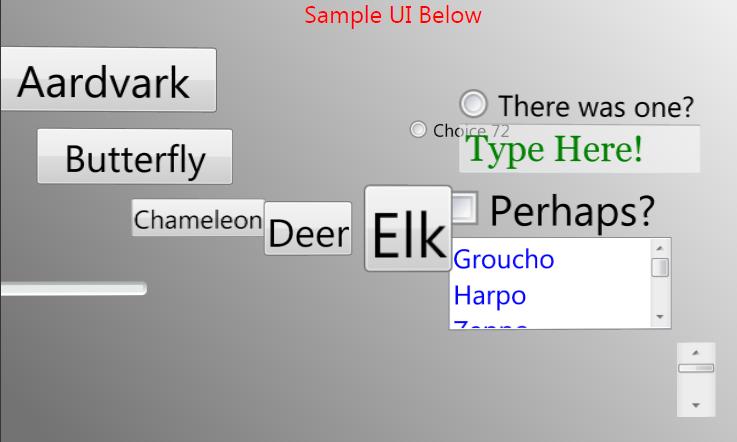
And this just completely breaks the illusion we're going for.
On the other hand, if we always use a camera distance that's too far from the subject, then at angles further away from 0° we don't get any sense of perspective or 3D-ness. Here are two examples of the same rotation angle, where the first has a camera reasonably near in, and the second has the camera at infinity. Believe it or not, both scenes are at the same rotation angle. We clearly need to stay away from the second one, as it really doesn't give any sense of perspective.
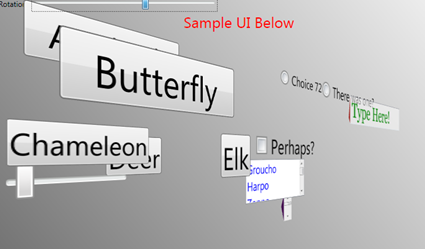
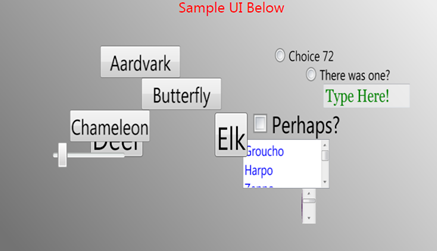
The solution we use here is to adjust the camera distance as we change our rotation. The camera distance moves towards infinity as we approach 0°, and it moves closer in as we approach some threshold rotation angle (the sample app chooses 90°). But it's not sufficient just to adjust the camera distance, since with a fixed FOV, the further back we move the camera, the more of the image that we catch in our "viewfinder". So, as we move forward and back, we also need to adjust our FOV to keep the same image cropping in the "viewfinder". This is like walking backwards with your camera and zooming in at the same time.
The following is a diagram demonstrating how FOV and camera distance can be coordinated in order to keep the same image section in view:
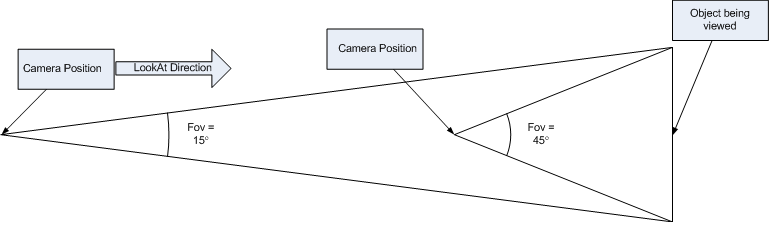
Once one sees the relationship there, and knows (from the previous post) how to derive distance from FOV, it becomes relatively simple to just adjust the FOV based on the ParallaxUI's rotation angle, knowing that that will result in pushing the camera backwards and forwards. Here's the code that the ParallaxUi uses to do this... nothing special, once the general principle is understood:
/// <summary>
/// Update the 3D rotation applied. As the angle approaches 0, bring the Field of View
/// of the camera towards 0 as well (making it more like an orthographic camera). This
/// is required so a face-on view will not show any signs of differences in z-values for
/// the different elements.
/// </summary>
private void RotChanged(Rotation3D rot, Point3D relativeCenter)
{
if (_vp3d != null)
{
// as the angle approaches 0, bring the Field of View towards 0
double absAngle = Math.Abs(GetAngle(rot));
const double defaultFov = 65.0;
const double angleThreshold = 90.0;
const double multiplierWithinThreshold = defaultFov / angleThreshold;
double fov;
if (absAngle < angleThreshold)
{
// x is the fraction of the angle within the threshold and within [0,1]
double x = absAngle / angleThreshold;
// makes descent into fov of 0 be non-linear, so less obvious jump. Requirement for this
// calculation is that 0=>0, and 1=>1.
double factor = x * x;
fov = factor * angleThreshold * multiplierWithinThreshold;
fov = Math.Max(fov, 0.01);
}
else
{
fov = defaultFov;
}
… elided irrelevant stuff …
}
}