Shadowcasting in C#, Part Four
Last time we saw how many different ways there were to get the calculation of the top cell based on the top vector wrong. Today we'll take a briefer look at determining the bottom cell.
We know from our discussion of last time that the right way to determine what is the top-most visible cell in a column portion is to consider where the top vector leaves the column. By similar logic, the right way to determine where the bottom-most cell is in a column portion is to look at where the bottom vector enters the column. Clearly where the vector enters the current column is precisely the same place that it left the previous column, and we already know how to calculate that.
What sorts of things go wrong if you, say, round down instead of rounding to the cell where the vector enters the column? In my implementation of the other day I made a deliberate mistake: for the bottom direction vector I do the division and round down. This introduces some artifacts. For example, it means that you can see immediately behind nearby pillars but not behind far-away pillars:
Notice how the pillar to the left casts a full 90 degree shadow. However, the pillar to the right permits me to see the square immediately behind it, and then casts a shadow. This is not very realistic; if I can see immediately behind the pillar then why can I not also see beyond it?
Note that this also presents a gameplay problem. Suppose there was a monster "hiding" behind the pillar east of me there. I could see the monster, but it could not see me! If the targeting system for arrow attacks requires line-of-sight, and line-of-sight is determined by simply computing the whole field of view and checking whether the cell in question is in the field, then I can shoot the monster but it cannot shoot me. By similar logic, a monster that is two cells to the west of the pillar west of me can shoot me, but I cannot see it or shoot it.
Does this problem go away if we rewrite the rounding algorithm to be less permissive by rounding more appropriately? No! We still have a symmetry problem in a room full of pillars. Let's put both the "round down" and the "round to lowest column entry" algorithms next to each other for a comparison. Click on the control to play the game "in stereo":
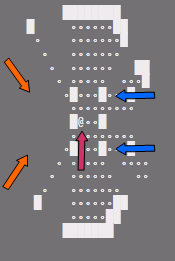
Notice how in both implementations it is possible to get into a position where you can see behind a pillar, but the monster standing there cannot see you:
Monsters standing at the blue arrow cells are visible from the player's location, but the monsters cannot see the player. Monsters standing at the orange arrow locations can see the player, but the player cannot see them.
The problem here is that the algorithm computes the set of cells where any point in the target cell is visible from the center of the player's cell. In order for the algorithm to be symmetric we need to allow any point in the target cell to be visible from any point in the player's cell. That is the "permissive field of view" algorithm. It uses the same concepts that we've described here; it progressively scans a region (a quadrant, rather than an octant) and keeps a set of line segments (not vectors, since they need not go through the origin) that track what regions are in view as you get farther and farther away from the origin. It's a rather tricky algorithm to get right, and so I'm not going to present it here.
Next time: Now that we know how to compute the top and bottom cells, actually running the algorithm is pretty straightforward. We'll go through the details of the code.