Graph Colouring, Part Five
I said last time that I was interested in finding colourings for graphs that have lots of fully connected subgraphs, aka "cliques". For instance, I'd like to find a four-colouring for this sixteen-node graph:
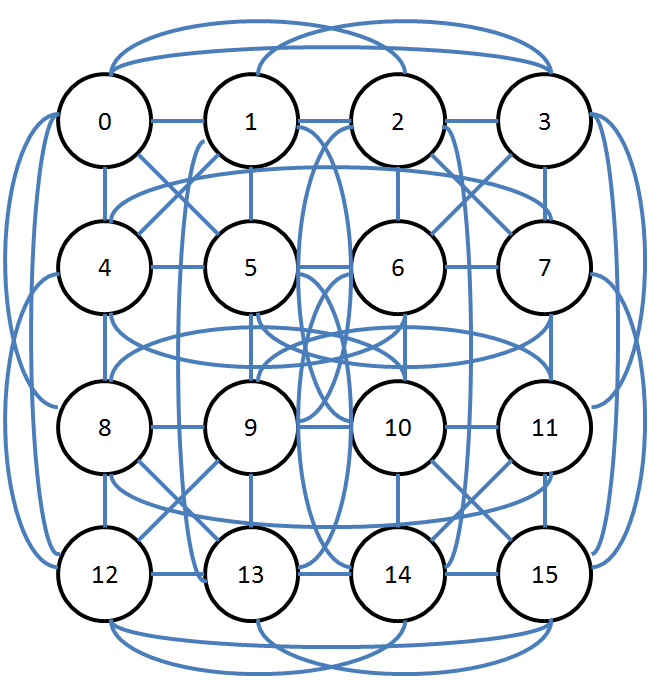
Yuck. What a mess.
What this graph is doing a bad job of conveying is that there are twelve fully connected subsets. {0, 1, 2, 3} forms a clique. So does {0, 1, 4, 5}. And so does {0, 4, 8, 12}.
It would be great if I had a better way to display full connectedness. How about this: I'll just draw a dotted ellipse around a fully connected subset, and you can then mentally fill in all the edges:
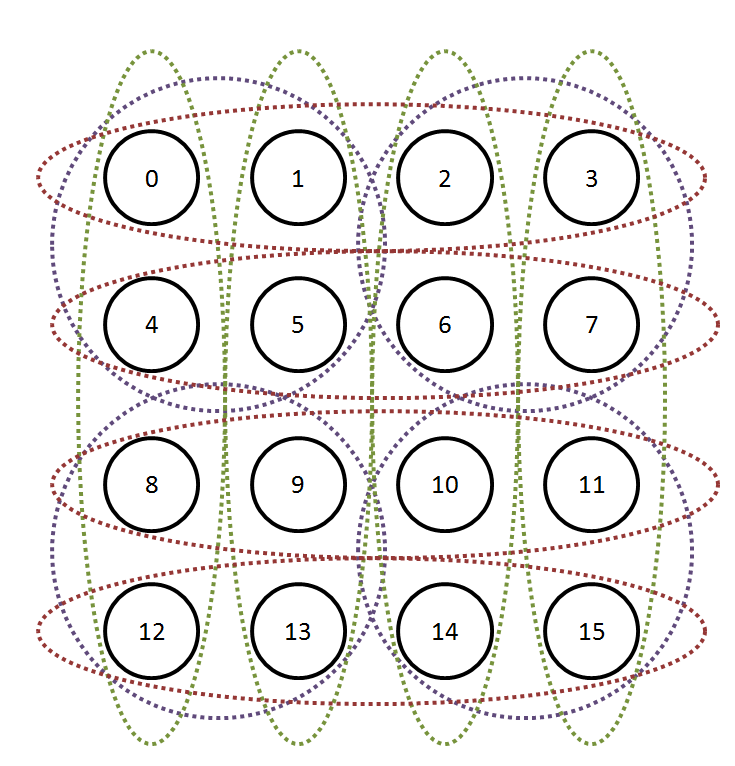
Hmm. That might not actually be better.
Anyway, you get the idea. What would be really nice is if I had a way to cleanly represent this in code. What I want to do is somehow take the concept of a sequence of fully connected subsets:
{0, 1, 2, 3}, {4, 5, 6, 7}, {8, 9, 10, 11}, {12, 13, 14, 15},
{0, 4, 8, 12}, {1, 5, 9, 13}, {2, 6, 10, 14}, {3, 7, 11, 15},
{0, 1, 4, 5}, {2, 3, 6, 7}, {8, 9, 12, 13}, {10, 11, 14, 15}
and turn that into a list of edges: {0, 1}, {0, 2}, {0, 3}, {1, 0}, {1, 2}, ...
If I end up with some of the edges on the list twice, who cares? I've implemented my graph as a Boolean array; no problem if I set one of the entries to true twice.
This is easily done with LINQ:
public static IEnumerable<Tuple<int, int>> CliquesToEdges(IEnumerable<IEnumerable<int>> cliques)
{
return
from clique in cliques
from item1 in clique
from item2 in clique
where item1 != item2
select Tuple.Create(item1, item2);
}
Now, I suppose we could just make an array of arrays with all the numbers I listed above. But notice somthing about the pattern:
In that first line, we start with {0, 1, 2, 3}. Then we add four to each: {4, 5, 6, 7}. Then we add eight: {8, 9, 10, 11}. Then we add twelve: {12, 13, 14, 15}.
In the second line, we start with {0, 4, 8, 12}. Then we add one: {1, 5, 9, 13}. Then we add two. Then three.
In the third line, we start with {0, 1, 4, 5}. Then we add two, eight and ten.
In short, we could write a generator for the subsets if we wanted to, by noting down the patterns:
var offsets = new[,] {
/*rows*/ {new[] {0, 4, 8, 12}, new[] {0, 1, 2, 3 }},
/*columns*/ {new[] {0, 1, 2, 3}, new[] {0, 4, 8, 12}},
/*squares */{new[] {0, 2, 8, 10}, new[] {0, 1, 4, 5}}};
var cliques =
from r in Enumerable.Range(0, 3)
from i in offsets[r, 0]
select (from j in offsets[r, 1] select i + j);
var edges = CliquesToEdges(cliques);
var graph = new Graph(16, edges);
var solver = new Solver(graph, 4);
And if we solve that we get the colours 0, 1, 2, 3, 2, 3, 0, 1, 1, 0, 3, 2, 3, 2, 1, 0 for the 16 nodes:
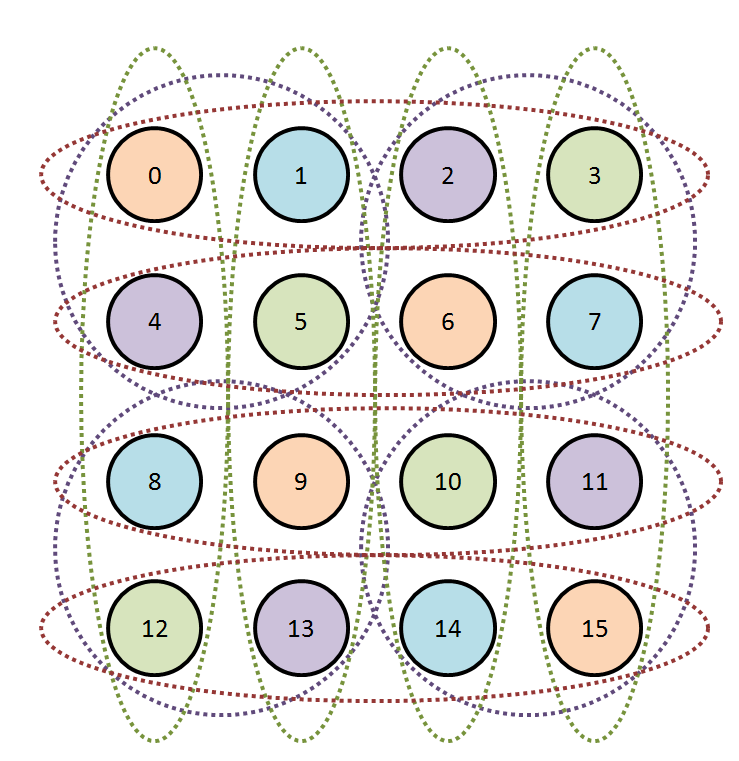
And sure enough, every fully-connected subset with an ellipse around it has no two nodes of the same colour. Neat!
But let's not stop there! What if instead of sixteen nodes we had... eighty-one! And what if instead of twelve fully-connected subsets, we had... twenty-seven!
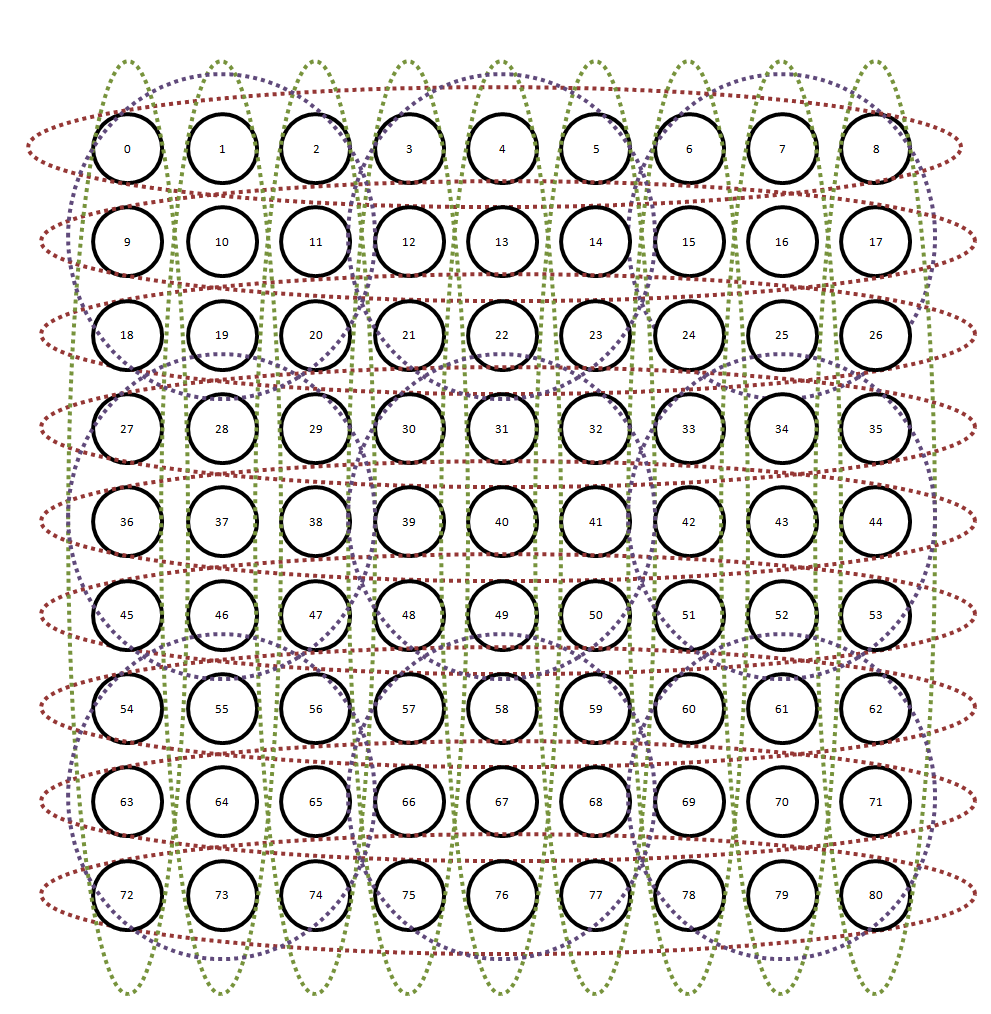
And what if we knew ahead of time what some, but not all of the colourings were?
First off, we can modify our subset generator easily enough:
var offsets = new[,] {
/*rows*/ {new[] {0, 9, 18, 27, 36, 45, 54, 63, 72}, new[] {0, 1, 2, 3, 4, 5, 6, 7, 8}},
/*columns*/{new[] {0, 1, 2, 3, 4, 5, 6, 7, 8}, new[] {0, 9, 18, 27, 36, 45, 54, 63, 72}},
/*boxes */ {new[] {0, 3, 6, 27, 30, 33, 54, 57, 60}, new[] {0, 1, 2, 9, 10, 11, 18, 19, 20}}};
The generation of the cliques and edges is the same. Let's make a solver for that graph and then restrict some of the colour choices ahead of time:
Graph graph = new Graph(81, edges);
var solver = new Solver(graph, 9);
string puzzle =
" 8 274 " +
" " +
" 6 38 52" +
" 32 " +
"1 7 4" +
" 92 " +
"78 62 1 " +
" " +
" 384 5 ";
int node = -1;
foreach (char c in puzzle)
{
++node;
if (c == ' ') continue;
solver = solver.SetColour(node, c - '1');
}
var result = solver.Solve();
int i = 0;
foreach (var r in result)
{
Console.Write(r + 1);
if (i % 9 == 8)
Console.WriteLine();
++i;
}
And we get the output
358127469
279654831
461389752
847916325
135278694
692435187
784562913
516793248
923841576
Holy goodness! There I was, minding my own business, trying to solve problems in graph theory and I accidentally made a Sudoku puzzle solver! Isn't it funny how life turns out sometimes? But that's just how awesome LINQ is.
And with that surprising result, I'm off to my ancestral homeland to spend a couple weeks visiting family and friends. We'll pick up with more Fabulous Adventures in September.