C++ Programming Interviews: What Interviewers Want You To Show
I recently passed a test on C/C++ and I like to share what I was challenged to to, what (and how) I responded. This post will seem like a lost chapter of the book Programming Interviews Exposed-Secrets to Landing Your Next Job, 2nd Edition [Mongan, Soujanen, Giguère; Wrox 2007].
I was asked to pseudo-code a function that returns the decimal equivalent to a roman numeral received as input. It seems like a trivial challenge but what the aspiring candidate must keep in mind, first of all, is the fact that the interviewer isn’t curious about your background with roman numerals. What he/she wants to check is your abilities in problem solving. Beside, the roman numeric system isn’t that trivial compared with the decimal system. It’s non-positional (in the sense that you don’t get ones in the last position, tens in the penultimate, hundreds in the position before, etc.). The system only contains symbols to represent powers of 10 (10n, n=0, …,3) and 5x10n (n=0, …,2) . Bizarre enough, huh?
Regarding those unusual features, the first thing I started doing was an exploration of typical equivalences, easy and not so easy roman numeral cases with their expected result. Those served me to both, craft the algorithm toward the general case and test my derived solution for correctness.
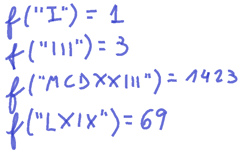
Those and some few other examples help us determine some basic syntax rules in roman numerals. Rules like repetition of characters (III, CC, XXX, …); subtraction (IX, CD, …); etc.
Those same rules have their own limitations, for instance
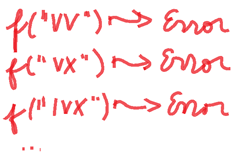
In other words, repetition is only allowed to characters I, X, C and M (1, 10, 100 and 1000 respectively) but not to V, L, D (5, 50, 500 respectively) and -while not represented in these examples- it can’t happen more than three times either. Subtracting V, L or D isn’t allowed either. Likewise, the 3rd erroneous example shows that we can get a character subtracting its immediate follower, but this latter can’t subtract to a third one (that is to say, a subtracting portion in a whole roman numeral only involves two characters).
Talk about all these like thinking in loud voice, while you write down in some margin (whiteboard, piece of paper) the rules you discover. If available using two different colors to separate DO’s and DON’T’s.
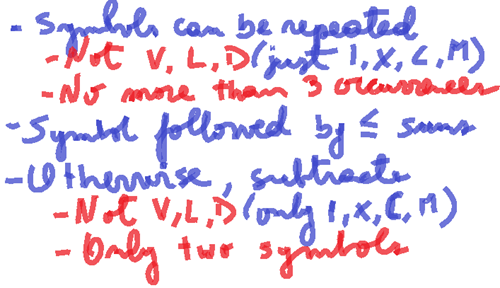
There are yet other syntax rules but, with my interviewer, we agreed to stop here.
Let’s start shaping the function skeleton, its public interface and expected return types
unsigned int rtoi(const wstring& romanStr) {
...
}
The function name, rtoi(), was chosen for its similarity in intention with atoi(). There are several decisions to explain here:
The returned type was chosen as unsigned int. Roman numerals don’t consider neither 0 (zero) nor negative numbers. For that reason, I wanted to make sure that the returned type were as restrictive as possible.
It may be argued that by allowing all kind of int, we could have taken the convention of using negative numbers to represent errors like invalid inputs, etc. But the drawback of that approach is that the caller of the function will have to take the precaution of explicitly asking for error conditions coming with the output. If the caller fails to check this out and just used the result instead, the execution would get an undetermined state.
That’s why I preferred to escalate an error by throwing values from an enumeration as in here
enum RomanConversionError {
IllegalSymbol, // input contains a symbol other than I, V, X, L, C, D, M
IllegalRepetition, // I, X, C, M repeated more than three times, or any other symbol repeated
IllegalSubtraction // V, L, D can't subtract
};
Some authors have arguments against throwing values before errors, especially when the function is intended to validate user input. But in my case this function is just a library function: it may be called by a UI validator object or by another component not necessarily related with user input.
- Regarding the input argument, the reader might wonder why to declare it as const. The fact is that this function won’t modify its input in any way. Therefore, is not a mal idea to enforce that so if tomorrow, as a consequence of maintenance, any programmer modified the input declared as constant, the application wouldn’t compile.
- Another aspect considering the input string is the fact that I chose it as wstring instead of simply string type. The fact is that most systems nowadays work with expanded character sets (typically UNICODE), as they better handle internationalization in currently Internet-enabled, interconnected age. You don’t have to reason like me here, as long as you are able to understand the context where your decisions are being taken. A wrong decision, though, would have been preferring string for simplicity: from a programming perspective, both types are siblings, specializing a common STL type called basic_string (with char and wchar_t, depending on the simple or expanded case). In fact, if the interviewer asked you about a generic solution, that would come as follows:
template<typename Ch> unsigned int rtoi(const basic_string<Ch>& romanStr) {
...
}
Yet one may argue about the decision of using the STL version of strings instead of the C-style, 0 (zero)-terminated char arrays. The decision in favor of the STL ones was based on the fact that they encapsulate a lot of the functionality a string must accomplish in order to be considered safe. For instance, a wchar_t* counterpart of our wstring could have come without the expected binary 0 (zero) ending char, leading to a potential buffer overrun. An STL-based string doesn’t have this problem because it handles its own memory (first reason), and its length isn’t based on a potentially missed ending char. STL strings are safer than their C-style counterparts, what doesn’t mean they are safe. They are just less error-prone and therefore recommended by several authors. They may impose certain overhead but in most of cases that overhead won’t be absent in high quality, defensive-coding version using C-style strings. It’s just a matter of deciding whether you programmer want to be responsible of that overhead or take advantage of those already baked versions that the STL put available for you.
- A last comment, prior to move inside the function itself, is the fact that the string argument is passed as a reference (by adding the ampersand modifier). It’s a matter of efficiency: if the ampersand was not present, the string would be passed by value, being copied to the stack with the consequent overhead. I’d rather avoid that.
All these said, let’s go through the function. I’ll finally implement here a generic version (now that I’ve mentioned that possibility)
template<typename Ch> unsigned int rtoi(const basic_string<Ch>& romanStr) {
int result = 0; /* value to return */
Additive currentAdditive;
unsigned int repeatedTimes;
Ch lastSymbol = L'\0', currentSymbol, nextSymbol;
/* main computing loop: inside reasonable length and without reaching the
end of the null terminated string */
for (typename basic_string<Ch>::const_iterator iter = romanStr.begin(),
iterNext;
iter!=romanStr.end();
iter+= currentAdditive.size,
result+= currentAdditive.value) {
currentSymbol = *iter;
/* Rule 1: Repetition. Can't happen more than three times and not every
symbol is repeatable */
if (lastSymbol==currentSymbol) {
if ((++repeatedTimes==4)||(isNotRepeatable(currentSymbol))) {
throw IllegalRepetition;
}
} else {
repeatedTimes = 1;
lastSymbol = currentSymbol;
}
/* the current symbol plus its follower (if not at the end) are
evaluated in getNexAdditive() to see how much to cumulate*/
nextSymbol = ((iterNext = iter+1)==romanStr.end()) ? L'0' : *(iterNext);
currentAdditive = getNextAdditive(currentSymbol, nextSymbol);
}
return result;
}
In few words, this function consists in a loop through all the input string chars. For each char we check whether it repeats or not the last one (in case it does, we control that repeated chars don’t reach 4 times). We also make sure that not every symbol is allowed to be repeated by calling the inline function isNotRepeatable(…) –defined as follow:
template<typename Ch> inline bool isNotRepeatable(Ch c) {
return ((c==L'V')||(c==L'L')||(c==L'D'));
}
By making it inline, we are instructing the compiler to avoid making any explicit call involving the stack. Instead this code will be spanned in the calling method, making the proper variable substitution. We could have defined a macro this way
#define isNotRepeatable(c) (((c)==L'V')||((c)==L'L')||((c)==L'D'))
but in that case we have less control on data being passed/received. An inline function is a better practice and presumably won’t involve the overhead of a true function call.
The iteration then locates the symbol next to the one being analyzed in the current iteration, and passes both to the function getNextAdditive(…). The purpose of that function, given those two symbols, is to determine whether both should be combined in a subtraction (the typical case of IV, where I is being subtracted from V for instance), or a case like VI, where only the V will be considered for the iteration, discarding the I (which will be picked up by the next iteration).
Thus, the output of this function is a struct defined as follows
typedef struct Additive {
unsigned int value, size;
} Additive;
As the reader may see, the value member contains the value to be added to the ongoing result. The size member, instead, will contain either 1 or 2 depending on whether both symbols were considered (as a subtraction) or only the first one while the other was ignored. Those two activities can be seen as the ending portion of the for loop.
Let’s complete the implementation by defining getNextAdditive(…) function:
template<class Ch> Additive getNextAdditive(
const Ch firstRomanChar, const Ch follower) {
Additive result;
result.size = 1; // default size
switch (firstRomanChar) {
case L'I':
switch (follower) {
case L'V':
/* I (1) subtracting to V (5) results in 4 */
result.value = 4;
/* a subtraction involves 2 symbols, so size is 2 */
result.size = 2;
break;
case L'X':
result.value = 9;
result.size = 2;
break;
case L'L':
case L'C':
case L'D':
case L'M':
/* a subtractor can't be less than a 10% of its follower
(i.e.: 99, IC wrong; must be XCIX) */
throw IllegalSubtraction;
default:
result.value = 1; /* follower ignored */
};
break;
case L'V':
/* V, L and D aren't subtractor in Roman numerals */
result.value = 5;
break;
case L'X':
switch (follower) {
case L'L':
result.value = 40;
result.size = 2;
break;
case L'C':
result.value = 90;
result.size = 2;
break;
case L'D':
case L'M':
throw IllegalSubtraction;
default:
result.value = 10;
};
break;
case L'L':
result.value = 50;
break;
case L'C':
switch (follower) {
case L'D':
result.size = 2;
result.value = 400;
break;
case L'M':
result.size = 2;
result.value = 900;
break;
default:
result.value = 100;
};
break;
case L'D':
result.value = 500;
break;
case L'M':
result.value = 1000;
break;
default:
throw IllegalSymbol;
}
return result;
}
At a first glance this function could look overwhelming, but the reader will immediately discover that it’s logic is pretty basic and repetitive, despite all the possible cases.
Before the interviewer, for completeness, it follows an analysis of the border conditions. For instance, what if the string received as arguments is empty (equivalent to “”)? In our case, the function will return 0. It could have also thrown an exception as well, but I’d rather preferred the former option.
We should also test the cases evaluated initially, in order to confirm/tune up the algorithm. I’ve already done it, but I leave those to the reader as an exercise.
From the algorithm itself we could conclude that its order is linear to the length of the input. Or, in other words, its complexity is O(n) , n being the length of the input, which is pretty much acceptable. Complexities to be avoided whenever possible are quadratic ones –O(n2) - or higher, or even exponential ones.
A production-ready implementation of this function, together with tons of test cases plus an inverse function itor(…) –which takes an integer and returns its roman equivalent- is offered here.