Audio Fidelity: Clipping
In theory, an audio signal can take on any amplitude. There is no mathematical upper limit for how far from zero a sample can go, or how high the magnitude of a continuous wave can go. In practice, however, a digital signal's amplitude is limited by its number of bits, and even electrical components can only handle so much voltage without being damaged. Every real-world device has some practical maximum value that the signal can attain. Try to go past this maximum, and your signal will suffer. Clipping occurs when an audio device tries to output a signal whose amplitude is greater than its maximum value, and instead outputs the maximum value. Clipped waves have a characteristic "leveled off" top (or bottom) that looks as if the wave were just chopped off.
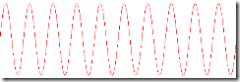
The best way to describe the problem with clipping might be by example. Here is a generic sine wave (click for larger image):
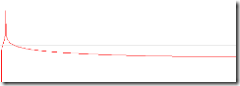
And here is the logarithmic frequency spectrum of that sine wave. The gray line represents a typical noise floor. Anything above the line is above the noise floor, and anything below the line generally won't be heard. As expected with a clear sine wave, we see a single spike at our fundamental frequency, and no other audible tones.
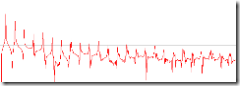
Now, here is the same sine wave doubled in amplitude and then clipped (admittedly, an extreme case, but not as uncommon as you'd think):
And the FFT of our clipped wave. Notice the clearly audible harmonics.
This is obviously a suboptimal listening experience - For every sound, you hear every odd harmonic. But it could be much worse. There is no good solution to limiting a signal level, and clipping is just one of several things that a filter can do when it tries to produce a signal that is too hot. A much worse outcome (common in poorly designed older digital filters which store samples as CPU integers) will overflow and "wrap" instead of clipping. The sample jumps from INT_MAX to INT_MIN (or vice versa), and the speakers represent this as a full-scale impulse, resulting in a "pop" that can damage your hardware (and your ears!).
One alternative to clipping, known as soft clipping, involves using a complicated function to "compress" the wave as it gets near the maximum value. Compressing the wave this way still introduces distortion, but it doesn't have the hard "edge" that clipping does.
Clipping and soft clipping introduce errors into a signal. For this reason, you want to do it as little as possible during intermediate steps. With the new audio engine in Windows Vista, all internal signals are stored as floating point numbers. Valid output samples are between -1.0 and 1.0, but intermediate steps between digital filters can be outside that range, and the data type handles it just fine. At the last possible step, the audio engine performs another kind of limiting (which I'll let JJ describe), converting to integer (if necessary) and sending to the audio codec. This is an improvement over all integer digital processing, which has to apply limiting at each stage.