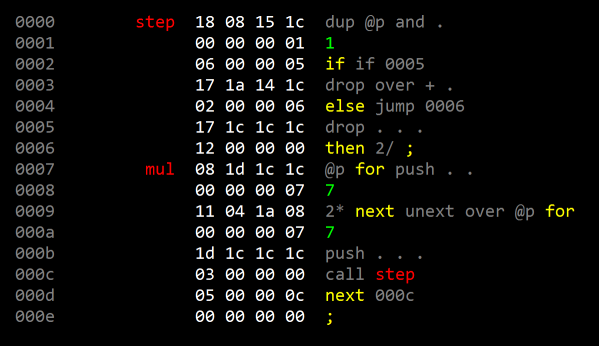
Multiply-step Instruction
Fourth in a series on colorForth and GreenArrays hardware. This time, how the multiply-step instruction works on the F18.
Bit Twiddling is Fun!
Here's a bit-twiddly interview question for you: Design an algorithm to multiply fixnum integers in O(log n) time using only addition. This may come in handy given that the F18 doesn't have a plain multiply instruction!
Starting with the primary school algorithm, but in binary:
110001
× 111101 110001
0000000
11000100
110001000
1100010000
+ 11000100000
101110101101****
<- 'bad' in hex :)
Summing the product of each digit of the multiplier (right to left) and the multiplicand; shifting (padding with zeros) as we go. Of course, single binary digit multiplication is super-easy; being just zero or the multiplicand itself.
Another way to formulate this is:
1 × 110001 << 0 = 110001
0 × 110001 << 1 = 0000000
1 × 110001 << 2 = 11000100
1 × 110001 << 3 = 110001000
1 × 110001 << 4 = 1100010000
+ 1 × 110001 << 5 = 11000100000
Or we can begin with the multiplicand shifted to the left and shift right after each step:
1 × 11000100000 >> 5 = 110001
0 × 11000100000 >> 4 = 0000000
1 × 11000100000 >> 3 = 11000100
1 × 11000100000 >> 2 = 110001000
1 × 11000100000 >> 1 = 1100010000
+ 1 × 11000100000 >> 0 = 11000100000
This leads to realizing that In fact we can do it in place. We can begin with the multiplier in the right-most bits, processing one bit at a time, shifting right after conditionally adding the left-shifted multiplicand. Pretty slick!
 |
 |
This code works with a pair of 8-bit values; first preparing by shifting the multiplicand 8 bits to the left, then performing 8 'step' operations. Each 'step' adds the multiplier if the low bit is set, then (always) shifts everything right. There you have it; multiplication in terms of only addition and shifting!
| 0000000000111101 | Left initially zero, right multiplier. |
| 00110001001111010001100010011110 | Add multiplicand (left - 110001).Then shift right. |
| 00011000100111100000110001001111 | Don't add (zero bit).Shift right. |
00111101010011110001111010100111 |
Add multiplicand (one bit)Shift right. |
| 01001111101001110010011111010011 | Add multiplicand.Shift right. |
| 01011000110100110010110001101001 | Add multiplicand.Shift right. |
| 01011101011010010010111010110100 | Add multiplicand.Shift right. |
| 00101110101101000001011101011010 | Don't add (zero bit).Shift right. |
| 00010111010110100000101110101101 | Don't add (zero bit).Shift right. And we're done! |
The Multiply-step Instruction
This is essentially how the F18 works. There is a multiply-step ( +* ) instruction that carries out one step of this process; applied n-times (usually in a micronext loop) to perform an n-bit multiply. You can read the details in the doc. The multiplier is placed in A, the multiplicand in S and an initial zero in T. Together, T and A are treated as a single shift register (like the left/right in our example above). Then a series of multiply-step ( +* ) instructions are executed; leaving the result (in A). Here's Greg Bailey's excellent description from the GreenArrays arrayForth Institute course:
[View:https://www.youtube.com/watch?v=RFN_SJ4Qw1Q&feature=youtu.be]
As he says, there are other purposes for the +* instruction. We'll get into them later.
Examples
Here's an example (note that the sim we're using is 32- rather than 18-bit, thus the 1f loop count)
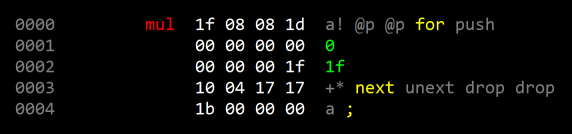 |
It may be more efficient to unroll the loop:
 |
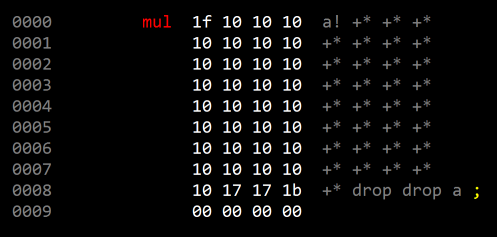 |
Or a good balance might be to do sets of three +* in a micronext loop:
 |
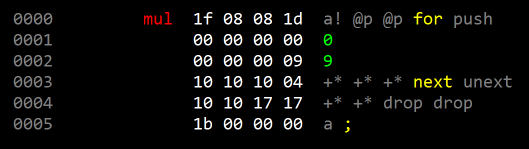 |
Try it out with some silly hex words:
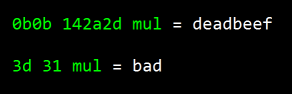 |
Have fun!