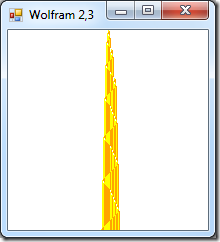
Wolfram – A New Kind of Turing Machine
Stephen Wolfram’s book, “A New Kind of Science” is flippin’ brilliant! (or perhaps I'm just not brilliant enough to realize he's a mad man) 1,280 pages packed with beautiful insights and Tufte-worthy visualizations. I remember discovering it while randomly browsing the MS library one day. I became so enthralled, an hour passed just standing there reading it! [I should also plug his excellent TED talk]
Just one of the bazillions of wonderful things covered is this simplest possible universal Turing machine. It was proved to be the lower limit on Turing machine universality by Alex Smith in 2007.
The tape head can be in one of two states (up/down) and the tape position may be one of three colors (white/yellow/orange). Of course, Alan Turing’s original allowed an unspecified finite number of states and symbols. The rules for Wolfram’s 2,3 machine are:
For example, the first rule says when in the up state and pointing at orange, then paint yellow, remain up and move to the left. On the other hand, if conditions are the same but in the down state (4th rule) then paint white and move to the right. Starting with a blank (white) tape it produces the following sequence of tape states (nice animation here):
Here’s a quick F# implimentation:
open System.Drawing
open System.Windows.Forms
let w = 200
let h = 1000
let b = new Bitmap(w, h)
let tape = Array.create w 0
let rec machine head state y =
let rules = function
| 1, 2 -> 1, 1, –1
| 1, 1 -> 1, 2, –1
| 1, 0 -> 2, 1, 1
| 2, 2 -> 1, 0, 1
| 2, 1 -> 2, 2, 1
| 2, 0 -> 1, 2, –1
let state', color, offset = rules (state, tape.[head])
tape.[head] <- color
Array.iteri (fun x c -> b.SetPixel(x, y,
match c with 0 -> Color.White | 1 -> Color.Yellow | 2 -> Color.Orange)) tape
if y + 1 < h then machine (head + offset) state' (y + 1)
machine (w / 2) 1 0
let form = new Form(Text="Wolfram 2,3", ClientSize=new Size(w, h), Visible=true)
form.Paint.Add(fun a -> a.Graphics.DrawImage(b, 0, 0))
Application.Run(form)