Recursion Is The New Iteration

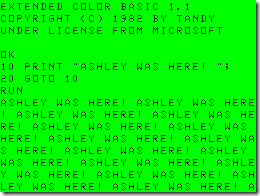
I remember the strange feeling as a kid the first time I saw structured BASIC after having been doing everything with line numbers. Any time I happened to walk into a Radio Shack in the early 80s I’d just have to leave this behind: 

I was in a GOTO/GOSUB world (give it a try). The first time I saw structured programming I thought, “How in the world can you program without line numbers?!” Seriously! What a silly kid.

Now as a silly adult, I’ve moved on to functional languages and have learned to live without some of the looping control flow statements that I took for granted in structured programming. How do you possibly program without for and while loops? Except for some constant expression like while(true){ … }, these make little sense without mutation.

It’s hardly noticed in some languages like XSLT because generally the transformation is driven by the data and you don’t often have the need for arbitrary loops. Instead you are generally iterating over the input elements (with <xslt:apply-templates … /> or <xslt:for-each …>) neither of which rely on assignment.

Recursive Definition of Iteration

Consider the good ol’ factorial function (in Scheme this time):

( define ( factorial n )
( if ( <= n 1 ) 1         ( * n ( factorial ( - n1 )))))

Recursively resolving to itself with ( - n1 ) until ( <= n 1 ) . Isn’t that inefficient? Doesn’t each recursive call create a new stack frame? The young imperative programmer in me gets the heebe jeebes looking at that!

Not all recursive expressions represent recursive behavior. In fact, iteration can be expressed recursively. One trick when considering the process that an expression represents is to think of functions as reducing to values rather than returning them. In a pure functional style (precisely because of referential transparency) you can do analysis by successive substitution. Let’s try it:

( factorial 7 )

… resolves to the definition, replacing the formal parameter n with 7:

( if ( <= 71 ) 1 ( * 7 ( factorial ( - 71 ))))

Since ( <= 71 ) is false, the if expression reduces to:

( * 7 ( factorial ( - 71 )))

… and further to:

( * 7 ( factorial6 ))

Continuing by the same process we get:

( * 7 ( if ( <= 61 ) 1 ( * 6 ( factorial ( - 61 )))))
( * 7 ( * 6 ( factorial ( - 61 ))))
( * 7 ( * 6 ( factorial5 )))  

You can see the pattern:

( * 7 ( * 6 ( * 5 ( factorial4 )))))
( * 7 ( * 6 ( * 5 ( * 4 ( factorial3 ))))))
( * 7 ( * 6 ( * 5 ( * 4 ( * 3 ( factorial2 )))))))
( * 7 ( * 6 ( * 5 ( * 4 ( * 3 ( * 2 ( factorial1 ))))))))  

And finally, ( factorial1 ) reduces simply to 1 because ( <= 11 ) is true. Now we have only to do plain multiplication to reduce to the final answer:

( * 7 ( * 6 ( * 5 ( * 4 ( * 3 ( * 21 ))))))
( * 7 ( * 6 ( * 5 ( * 4 ( * 32 )))))
( * 7 ( * 6 ( * 5 ( * 46 ))))
( * 7 ( * 6 ( * 524 )))
( * 7 ( * 6120 ))
( * 7720 ) 5040

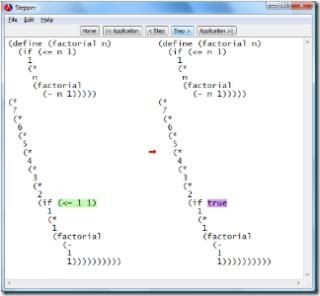
That’s it! Who needs a debugger? This is one of the nice things about expression-based rather than statement-based programming. There’s no state to watch change over time in a debugger. There is no concept of a timeline of state changes at all. It's more like solving an equation; only transformation of expressions into equivalent expressions until an answer is reached. It’s really cool to watch this in the “Stepper” (a substitution-based debugger) in DrScheme:

Look what happened with the factorial function though. It built up a bunch of deferred multiplications and then reduced them. Another analysis trick is to think of the length (width) of the expressions during the substitution process as space consumption and the number of transformations (height) as time consumption. Just look at the shape of the process. It grows wider, then narrows. In this case, factorial seems to have the space/time consumption profile of a recursive process – O(n) for both space and time. An iterative process should be O(1) with regard to space.

What we would rather is to express this in such a way that the recursive reduction is in tail position and can be thought of as a new set of formal parameters without external dependencies. A common technique is to use an accumulation parameter. How about we add this to the previous definition:

( define ( factorial n a )
( if ( <= n 1 ) a         ( factorial ( - n1 ) ( * na ))))

We add an extra parameter (a). Now if ( <= n 1 ) then we return the accumulated answer and otherwise recurse, pass along ( * na ) and no longer defer a bunch of multiplications; a small change, but watch the difference it makes (note, we seed it with 1 as the accumulated answer):

( factorial 7 1 )
( factorial ( - 71 ) ( * 71 ))
( factorial6 7 )
( factorial ( - 61 ) ( * 67 ))
( factorial5 42 )
( factorial ( - 51 ) ( * 542 ))
( factorial4 210 )
( factorial ( - 41 ) ( * 4210 ))
( factorial3 840 )
( factorial ( - 31 ) ( * 3840 ))
( factorial2 2520 )
( factorial ( - 21 ) ( * 22520 ))
( factorial1 5040 )
( factorial ( - 11 ) ( * 15040 ))
( factorial1 5040 )  

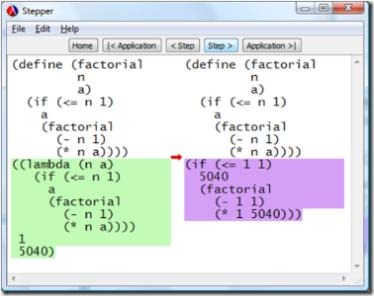
… and finally, because n is 1, it resolves to the accumulated answer: 5040. Nice!

This still takes O(n) time, but now it takes constant space. It’s iterative! Both definitions are recursive expressions but only one actually describes a recursive process.

Tail Call Optimization

So what happens when we try this in C#? What we’d hope is that the compiler and CLR would do proper tail call optimization (TCO).

using System;

publicstaticclassTail {
    publicstaticint Factorial( int n, int a) {
        if (n <= 1) return a;
        return Factorial(n - 1, n * a); }

    publicstaticvoid Main() {
Factorial(7, 1); }}  

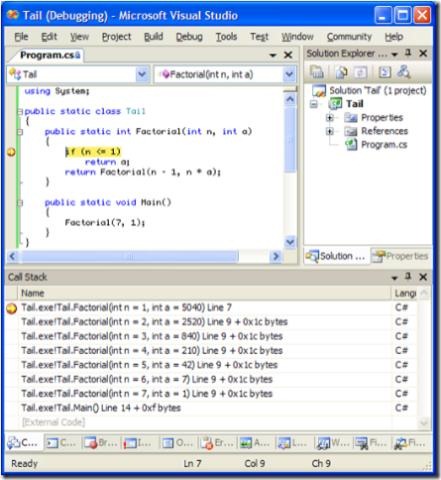
Watching in the debugger, you can see that a call stack is built and then collapsed even though this code is clearly tail recursive. It’s not being optimized.

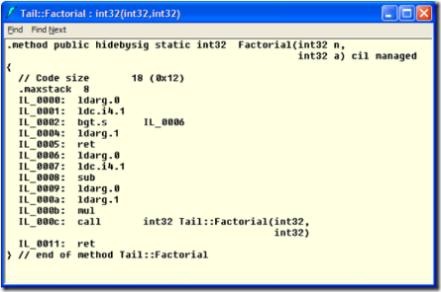
Looking at the IL for this we can see that it’s doing a regular “call” and “ret” – silly C# compiler!

Side note: This is enough to make my point, but the full story of the C# compiler and CLR is more complicated. If we want to get deep into how the CLR handles TCO we should talk about the .tail prefix in IL, differences between the 32- and 64-bit compilers, and the fact that at JIT-time even suboptimal IL may become tail optimized. For example, the above blows the stack in debug 32-bit builds, but is optimized properly in release 64-bit. Jomo Fisher has a nice post going into more details.

Tail recursion can be thought of as a “goto with parameters” and we can manually implement this if we like: 

publicstaticint Factorial( int n, int a) {
start:
    if (n <= 1) return a;
a *= n; n--;
    goto start; }

But how horribly ugly! Using mutation and goto! Notice also that if a *= n; and n--; were reversed it would be a bug. As soon as you introduce assignment, bugs like this are possible.    

Lets try this again in F# this time:

letrec Factorial n a =
    if n <= 1 then a
    else Factorial (n - 1) (n * a)
Factorial 7 1 

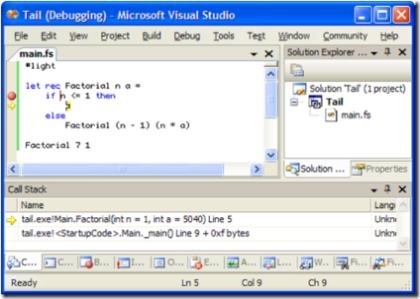
In the debugger, it’s apparently smart enough to eliminate the call stack! Excellent. 

Another side note: TCO makes debugging difficult. You can't walk back up the stack and inspect variables. For this reason, the F# compiler also doesn't do TCO in debug builds by default. Look at your Project/Build properties. There is a "Generate tail calls" checkbox.

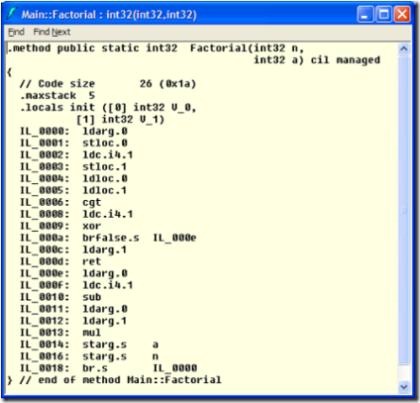
Let’s look at the IL: 

Sweet, the compiler is doing the “sub”, “mul” and stomping on the original arguments (“starg.s”), then simply branching (“br.s”) back to the beginning. I have no problem with compiler-generated mutation and goto.

Tail optimized recursion is no less efficient than iteration. I wish I had a dime for every time I've written for (int i = 0; i < x; i++) { … } These days it's the i++ that gives me the heebe jeebes.